CC Motor Closed Loop Control:
Steuerung der CC -Engine geschlossene Schleife – Das dynamische Verhalten eines Systems wird durch eine Reihe von Differentialgleichungen beschrieben. Bei zahlreichen Gelegenheiten erfordert die Lösung dieser Gleichungen die Bewertung der Integrale der Faltung, die eine schwierige Aufgabe sein kann.
In solchen Fällen wird eine einfachere Analyse durch die Verwendung von Übertragungsfunktionen unter Verwendung von Laplace -Transformationen durchgeführt.
Eine Übertragungsfunktion ist für lineare invariante Systeme wie das Verhältnis der Laplace -Transformation der Ausgangsvariablen in die Transformation der Eingangsvariablen unter der Annahme, dass alle Anfangsbedingungen Null sind.
Nichtlineare Systeme mit einem oder mehreren Parametern, die variieren, können keine Übertragungsfunktionen haben, da die Laplace-Transformation für sie nicht vorhanden ist. Trainingssysteme mit Nicht-Liesen können jedoch linearisiert werden und die lineare Rückmeldungstheorie kann jedoch angewendet werden.
Diese Systeme können durch Blockdiagramme oder Signalflussdiagramme dargestellt werden. Im Ansatz des Blockdiagramms repräsentiert ein Block die Funktion einer Komponente mit seiner Eingabe und seiner Ausgabe. Die Komponentenübertragungsfunktion ist im Block geschrieben. Somit ist die Übertragungsfunktion der Form
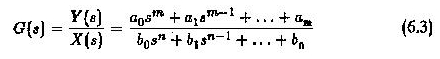
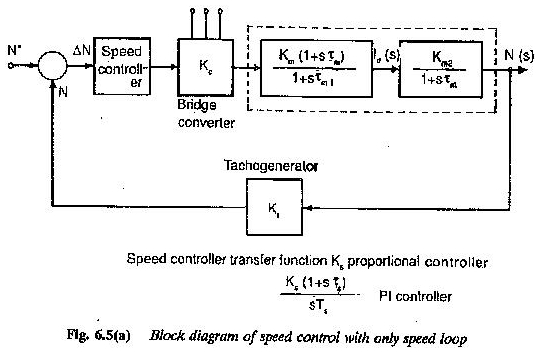
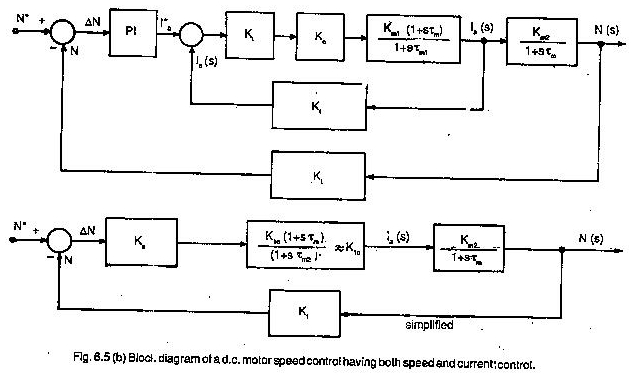
Während der Definition der Übertragungsfunktion wurde die Transformation von Laplace verwendet, da sie alle Differentialgleichungen in einfache algebraische Gleichungen verwandelt. Abbildung 6.5 repräsentiert ein Blockdiagramm eines DC -Motors in einem Antriebssystem.
Der Motor verfügt über eine Verstärkungsspannung als Eingangsvariable und Geschwindigkeit als Ausgangsvariable. Die Übertragungsfunktion ist im Block geschrieben.
Die Übertragungsfunktion stammt aus allen Differentialgleichungen, die das Verhalten des Systems beschreiben. Es geht jedoch nicht um die interne physikalische Struktur des Systems.
Verschiedene physikalische Systeme können ähnliche Übertragungsfunktionen und auch ein ähnliches dynamisches Verhalten haben. Die Übertragungsfunktion ist in Bezug auf Systemparameter und ist eine Systemeigenschaft. Es hängt nicht von der Größe oder der Art des Eingangs ab. Die höchste Kraft von S im Nenner repräsentiert die Reihenfolge des Systems.
Ein einfaches Beispiel finden Sie im Folgenden, um die Einfachheit der Übertragungsfunktionen zu zeigen.
Beispiel:
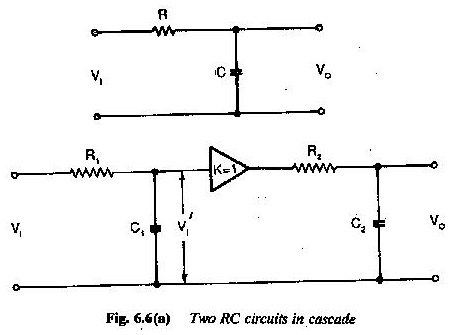
Zwei RC -Schaltungen sind in der Kaskade verbunden, wie in Abbildung 6.6 gezeigt.
Der Eintrag ist ein Schritt
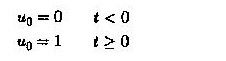 Der Verstärker wird verwendet, um als CC -Kopplung zwischen ihnen zu arbeiten. Bestimmen Sie die zeitliche Variation von U2. Wir wissen
Der Verstärker wird verwendet, um als CC -Kopplung zwischen ihnen zu arbeiten. Bestimmen Sie die zeitliche Variation von U2. Wir wissen
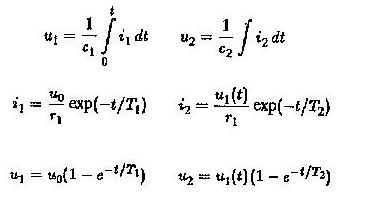
Das U2 / UO -Verhältnis wird durch Bewertung des Integrals der Faltung erhalten
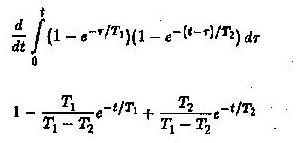
Wenn eine weitere RC -Schaltung in der Kaskade zum angegebenen Schaltkreis hinzugefügt wird, ist die Bewertung von U2 / U0 sehr schwierig.
Andererseits haben wir, wenn der Ansatz der Übertragungsfunktion verwendet wird
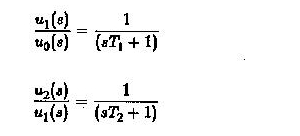
Durch die Verwendung dieser Gleichungen haben wir

kann sehr leicht bewertet werden

wie eine partielle Fraktionsausdehnung.