Übergangs -CC -Motoranalyse:
Start, Bremsen, Geschwindigkeitsänderung und Laständerung sind die transiente Analyse des kontinuierlichen Strommotors, der häufig in einem Industrieakteur auftritt.
Man ist daran interessiert zu wissen, wie sich der Strom, das Drehmoment und die Geschwindigkeit des Antriebsmotors im Laufe der Zeit in diesen Übergangsvorgängen verändern.
Man ist auch daran interessiert, Energieverluste zu kennen, insbesondere für diejenigen, die für die Motorheizung verantwortlich sind, und der Zeit, die für die Abschluss der transienten Analyse des DC -Motors benötigt wird.
Diese Informationen sind vom Designer erforderlich, um eine geeignete Notation des Motors, der Art und des Typs seiner Steuergeräte und des Betriebskalenders sowie der Arten von Schutzgeräten und deren Parametern auszuwählen.
Die dynamischen äquivalenten Schaltungen von CC -Motoren sind in Abbildung 5.12 dargestellt. Die Quellspannung V -Strom der IA- und Retract EMF Motorverstärkung werden durch Buchstaben am unteren Rand des Falles bezeichnet, um zu betonen, dass diese sofortigen Werte variabler Zeitmengen sind.
B und j sind jeweils der viskose Reibungskoeffizient in NM / rad / s und das polare Trägheitsmoment in kg-m2 des Motorsystems des Motors, der an der Motorwelle erwähnt wird.

Die Spannungsgleichung des Übergangsverstärkungskreises ist gegeben durch

Dynamik des Motorlastsystems

Weiter
![]()
Die obige Übergangsanalyse des Gleichstrommotors ist für jeden DC -Motor gültig. Im Falle eines angeregten Motors separat, wenn der Feldstrom konstant gehalten wird, bleibt der Durchfluss konstant und (5.16) und (5.17) sind lineare Differentialgleichungen.
Im Falle eines Serienmotors ist der Durchfluss aufgrund der Sättigung des Magnetkreises eine nichtlineare Funktion des Verstärkungsstroms und folglich (5.16) und (5.17) nichtlineare Differentialgleichungen.
Auch wenn der Magnetschalter angeblich durch Vernachlässigung der Sättigung linear ist, sind (5.16) und (5.17) nichtlineare Differentialgleichungen, da E proportional zum Produkt von IA und ωm und T proportional zu I2A ist.
Daher können diese Gleichungen für eine Reihe in Serien nicht digital durch die Rangkutta -Methode in 4. Ordnung oder die Prädiktorkorrektormethode aufgelöst werden.
Übergangsanalyse des angeregten Motors getrennt mit ungewöhnlicher Kontrolle:
Wenn der Feldstrom konstant gehalten wird, bleibt der Fluss konstant. Keφ -Ersatz durch eine Konstante K in den Gleichungen. (5.16) bis (5.18), gibt

Differenzierung der Gleichung. (5.20) gibt
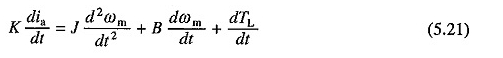
Ersetzen der Gleichung. (5.19) für DIA / DT von (5.21) und die Neuordnung, die die Begriffe geben
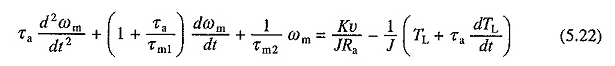
Differenzierung der Gleichung. (5.19) gibt

Ersetzen der Gleichung. (5.20) für Dωm / dt der Gleichung. (5.23) und die Begriffe neu organisieren
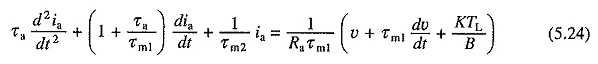
Oder


Die Gleichungen (5.22) und (5.24) sind zweite lineare Differentialgleichungen und können aufgelöst werden, wenn die entsprechenden Anfangsbedingungen bekannt sind. Sobald die IA -VS -Beziehung aus der Gleichung erhalten wird. (5.24) kann die Beziehung t vs t berechnet werden.
Übergangsanalyse des Beginns des angeregten Motors getrennt mit der Kontrolle der Verstärkung:
Eine Übergangsanalyse des Startprozesses wird hier in Betracht gezogen, um zu demonstrieren, wie die oben genannten Gleichungen verwendet werden.
Es wird angenommen, dass der Motor mit einer konstanten Spannung V durch seine Anschlüsse gegen ein konstantes Ladungsmoment TL und einen festen Widerstand in seinem Verstärkungskreis begonnen wird.
Es ist üblich anzunehmen, dass der Motor erst beginnt, nachdem sein entwickeltes Drehmoment das Ladedrehmoment überschreitet. Weil dieser Motorstrom den von ihm angegebenen Wert erreichen sollte

Wenn der Motor an die Stromversorgung angeschlossen ist, ist der Anfangswert des Stroms Null und aufgrund der Induktivität der ungewöhnlichen Schaltung dauert es eine bestimmte Zeit, um den Wert zu erreichen.
Während dieser gesamten Periode, die als erstes Intervall der Übergangsantwort qualifiziert wird, bleibt der Motor am Stopp und daher bleibt die hintere EMF Null. Der Motor verhält sich wie eine einfache RA – die Ladung. Deshalb wird seine Strömung durch gegeben

Das zweite transiente Antwortintervall beginnt, nachdem der Strom den Wert erreicht hat. Da V und TL Konstanten sind, sind DV / DT und DTL / DT Null. Ersetzen dieser Werte in Gleichungen. (5.22) und (5.24) gibt an
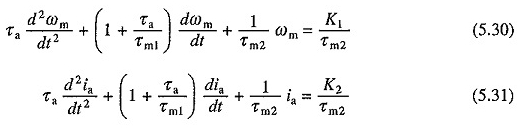
Oder
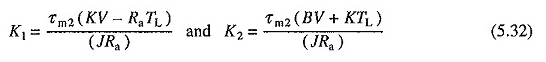
K1 und K2 repräsentieren die permanenten Geschwindigkeits- und Stromstrom mit einem Ladungsdrehmoment, der TL entspricht.
Anfangsbedingungen für die Lösung von Gleichungen erforderlich. (5.30) und (5.31) sind
![]()
Angesichts der Tatsache, dass das Motordrehmoment zu Beginn dieses Intervalls dem Lastdrehmoment aus der Gleichung entspricht. (5.17)

Weiter von der Gleichung entfernt. (5.16)

Gleiche Lösungen. (5.30) und (5.31) mit den von (5.33) bis (5.35) angegebenen Ausgangsbedingungen haben das Formular:

wobei α1 und α2 charakteristische Gleichungswurzeln sind und durch gegeben werden
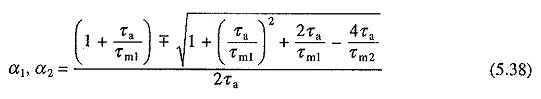
Beachten Sie, dass die obigen Gleichungen durch Messung der Zeit zu Beginn des zweiten Intervalls abgeleitet wurden.
Für Motoren von weniger als 1000 kW sind die Wurzeln α1 und α2 im Allgemeinen real.
Für größere und mittelgroße Motoren mit einer externen Induktivität, die im Verstärkungskreis verbunden ist, wie im Fall eines Hubschraubers und einer von einem DC -Motor gelieferten Übergangsanalyse können die Wurzeln komplex sein.
Die Art der ωm vs T- und Ia -VS -T -Kurven für Start -up -Transienten, wenn die Wurzeln real sind, sind in Abbildung 5.13 (a) dargestellt.
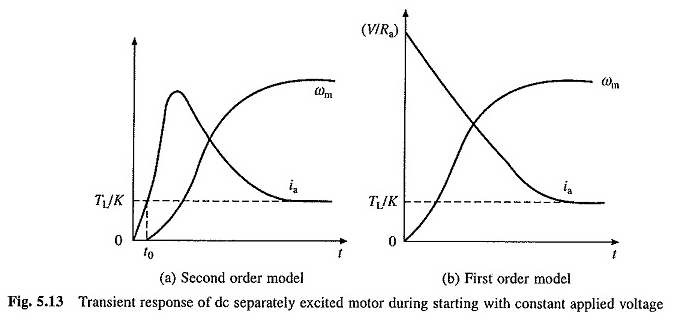
In kleinen Motoren ist τa aufgrund eines großen Widerstands gegen die Verwicklung der Verstärkung sehr klein. Es kann daher übersehen werden. Ersetzen von τa = 0 in den Gleichungen. (5.30) und (5.31) gibt
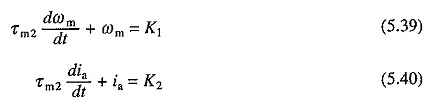
Aus τa = 0 geht der Strom in Nullzeit zum v / ra -Wert. Somit sind die Anfangsbedingungen
![]()
Gleiche Lösungen. (5.39) und (5.40) Ertrag

Die Art von ωm in Bezug auf die Kurven T und AI im Vergleich zu diesen Gleichungen ist in Abbildung 5.13 (6) dargestellt.
Übergangsanalyse der dynamischen Bremsung des angeregten Motors separat:
Es wird angenommen, dass eine konstante TL -aktive Last auf die Motorwelle wirkt. Übergangsgeschwindigkeit und Stromgleichungen können erhalten werden, indem ein neuer Wert für den Widerstand der ungewöhnlichen Schaltung und v = 0 in den Gleichungen ersetzt wird. (5.30) und (5.31). Es gibt

Auch hier – K3 und K4 repräsentieren jeweils Geschwindigkeits- und Stromwerte im Gleichgewichtszustand. Dieser dauerhafte Betrieb tritt auf, wenn das aktive TL -Ladedrehmoment zum Anfahren des Motors in die entgegengesetzte Richtung bewirkt ist. Die für die Lösung dieser Gleichungen erforderlichen Anfangsbedingungen werden wie folgt erhalten:
Es wird angenommen, dass der Motor bei der Einleitung des Brems im Gleichgewichtszustand mit einem TL -Lastdrehmoment betrieben wurde. Dann aus der Gleichung. (5.30)
![]()
Für einen allgemeinen Fall muss K1 als Anfangsgeschwindigkeit angesehen werden.
Das Bremsen kann mit oder ohne Öffnen des Verstärkungskreislaufs aufgetragen werden. Wenn es nicht geöffnet ist und das Automobil zum Bremsen übergeht, wird die Kontinuität des Verstärkungsstroms beibehalten, dann der Anfangswert des Stroms aus der Gleichung. (5.31), wird K2 sein.
Wenn es jedoch geöffnet ist, ist der Anfangswert des Stroms Null. Hier gehen wir davon aus, dass es während des Übergangs offen ist. ALSO
![]()
Jetzt von Gl. (5.19) und (5.20) durch Ersetzen von V = 0, Ia = 0 und ωm = K1.
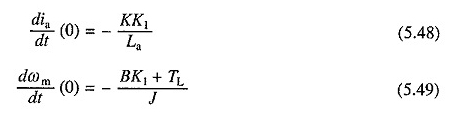
Gleiche Lösungen. (5.43) und (5.44) mit den Anfangsbedingungen von (5.46) bis (5.49) haben das Formular:
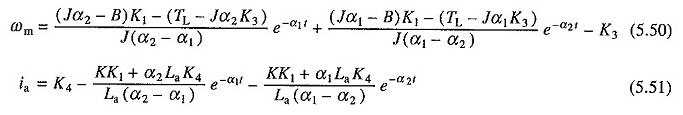
wobei α1 und α2 durch die Gleichung angegeben sind. (5.38).
Die Art der transienten Reaktion unter dynamischem Bremsen für den Fall von realem α1 und α2 ist in Abbildung 5.14 dargestellt.
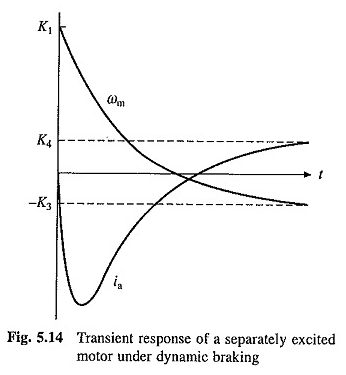
Die Übergangsgleichungen des Stecker -In -Betriebs werden aus (5.19), (5.20), (5.22) und (5.24) ermittelt – V für v.
Energieverluste während des Übergangsbetriebs:
Energieverluste im Motor und in den Widerständen im Motorverstärkungskreis sind bei der vorübergehenden Betriebszeit erforderlich, um geeignete Anmerkungen des Motors und des Widerstands auszuwählen. Sie sind auch notwendig, um die Effizienz und Effizienz des Übergangsprozesses zu berechnen.
Multiplizieren Sie beide Seiten der Gleichung. (5.16) durch IA gibt

Da das viskose Reibdrehmoment Teil des TL -Lastdrehmoments ist, haben wir Gleichung. (5.17)

Gleichungen ersetzen. (5.18) und (5.53) in (5.52) und die Integration der beiden Seiten der resultierenden Gleichung gegen die Zeitrendite
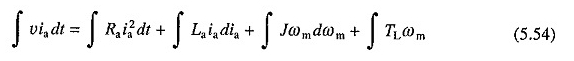
Diese Gleichung sieht vor, dass bei der Gesamtenergie, die die Quelle während eines Übergangsprozesses bereitstellt, ein Teil im Widerstand des Verstärkungskreislaufs verschwendet wird, der zweite Teil in der Induktivität des Verstärkungskreises gespeichert wird. Der dritte Teil wird in der Trägheit der mechanischen Teile gespeichert und der Rest wird von der Last verbraucht.
Die Energie, die in der Induktivität des Verstärkungskreislaufs gespeichert ist, ist im Vergleich zu anderen Energiebegleitern im Allgemeinen niedrig und wird daher in der späteren Analyse vernachlässigt.
Das Starten des Motors mit einer konstanten V -Spannung V und dem TL -Ladedrehmoment wird nun jetzt berücksichtigt.
Aus

wobei ωm0 die ideale Geschwindigkeit ohne Last ist. Gleichungen. (5,54) und (5.55)

Die Gleichung (5.56) ergibt einen Ausdruck für den Energieverlust im Widerstand des Verstärkungskreislaufs der Maschine. Bei Beginn ohne Last beträgt die endgültige Geschwindigkeit (Gleichgewichtszustand) ωm0. Daher ist der Energieverlust in jeder E0 -Lastbedingung

Es ist interessant festzustellen, dass der Energieverlust im Motorverstärkungskreis während des Start -up ohne Last der kinetischen Energie entspricht, die in den Drehsteilen des Motors mit einer stabilen Zustandsgeschwindigkeit gespeichert ist.
Darüber hinaus ist es unabhängig von der Dauer des Startprozesses, der Art der Kükengeschwindigkeit und der Eigenschaften des Motorgeschwindigkeitsstroms, der Anzahl der Stufen des Startwiderstands und des Werts der Reister in jedem Schritt.
Da sich ωm0 nicht sehr von der Geschwindigkeit im Gleichgewichtszustand unterscheidet, wobei die TL -Last auf der Motorwelle der erste Term auf RHS der Gleichung ist. .
Der zweite Term hängt von den Eigenschaften der Motorgeschwindigkeitslast und dem Wert des Startwiderstands ab. Dieser Begriff wird durch den schattierten Bereich von Abbildung 5.15 dargestellt.

Wie oben angegeben, bleibt der erste Term auf der rechten Seite von (5,56) unverändert mit der Änderung des Startwiderstands. Es kann jedoch durch eine reduzierte Start -up -Spannungsmethode gesenkt werden. Betrachten Sie den Fall, in dem die Quellspannung in einer Reihe gleicher Schritte angewendet wird. Der erste Teil des mth -Kupferverlusts wird sein
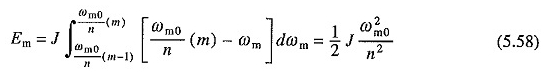
Da dieser Teil des Kupferverlusts in allen N -Schritten gleich sein wird, wird insgesamt kein Kupferverlust während des Starts

Vergleich mit der Gleichung. (5.57) zeigt, dass der Kupferverlust ohne Last um den Faktor n reduziert wurde.
Lassen Sie uns dann den Verlust während der rheostatischen Bremsung untersuchen. Durch Ersetzen von V = 0, durch Vernachlässigung und Annahme, dass das Lastdrehmoment konstant und gleich TL ist, kann die folgende Gleichung von (5.52) und (5.53) abgeleitet werden.
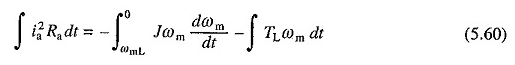
Es wurde angenommen, dass vor dem Bremsen der Motor im Gleichgewichtszustand gegen ein passives Ladungsmoment TL mit einer ωml -Geschwindigkeit betrieben wurde. Zur EQ -Integration. (5.60) gerendert

Diese Gleichung zeigt an, dass die Last einen Teil der gespeicherten kinetischen Energie absorbiert und dass der Rest in Form eines Kupferverlustes abgeleitet wird.
Zum Verstopfen bei der Substitution von – V für V und der = 0 in den Gleichungen. (5.52) und (5.53) Die folgende Gleichung wird für den Verlust von Kupfer erhalten
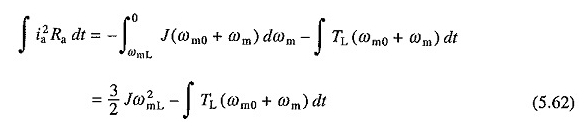
Gleichungen. (5.61) und (5.62) Kupferverluste ohne Last unter Bremsen und dynamischem Stecker sind 1/2 Jω20 bzw. 3/2 Jω20. Daher wird der Verlust während der Verbindung während der dynamischen Bremsung das Dreifache sein.
Da während der aus der kinetischen Energie der Drehstücke erhaltenen Steckerergie nur 1/2 Jω2m0 beträgt, wird der Rest Jω2m0 aus der Stromversorgung entnommen.
Übergangsanalyse des angeregten Motors getrennt mit der Feldsteuerung:
Entweder die konstante Verstärkungsspannung. JETZT
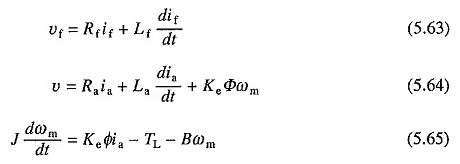
Hier ist φ eine nichtlineare Funktion von if. Wenn die Sättigung vernachlässigt wird und φ proportional zu SO sein soll (5.64) und (5.65) kann als geschrieben werden

wobei k ‚= Kekφ.
Aufgrund der Begriffe k’ifωm und k’ifia, die das Produkt von zwei Variablen (5,66) und (5,67) betreffen, sind nichtlineare Gleichungen, selbst wenn die Sättigung vernachlässigt wurde.
Daher kann diese Analyse mit digitalen Methoden zur Auflösung nichtlinearer Differentialgleichungen wie 4. Runege-Kutta und Predictive-Corners-Methoden durchgeführt werden.
Ein Sonderfall mit Landkontrolle tritt auf, wenn der Verstärkungsstrom konstant gehalten wird. Dann wird die Dynamik des Motorlastsystems durch die Gleichung beschrieben. (5.63) mit der folgenden Gleichung:

wobei Ka = Kekφia und IA der Strom der Verstärkung sind.
Der Gleichung. (5.68) Expression von if und DIF / DT kann erhalten werden. Ersetzen Sie sie in der Gleichung. (5.63) und reorganisieren die „Begriffe geben

Oder

Der Motor kann unter Verwendung der Gleichung auf seine Übergangsantwort analysiert werden. (5.69) vorausgesetzt, dass die Anfangsbedingungen bekannt sind. Der Anfangswert von ωm ist vom Betriebspunkt zum Gleichgewichtszustand unmittelbar vor den Transienten bekannt und der Anfangswert von dωm / dt wird aus der Gleichung berechnet. (5.68).

