Análisis de motores de transición CC:
Comenzar, frenado, cambio de velocidad y cambio de carga son el análisis transitorio del motor de corriente continua que ocurre comúnmente en un jugador industrial.
Uno está interesado en saber cómo el actual, el par y la velocidad del motor de conducción cambian con el tiempo en estas operaciones de transición.
Uno también está interesado en conocer las pérdidas de energía, en particular las responsables de la calefacción del motor y el tiempo tardado para completar el análisis transitorio del motor de CC.
El diseñador es necesario para seleccionar esta información para seleccionar una notación apropiada del motor, la naturaleza y el tipo de su equipo de control y su calendario operativo, y los tipos de dispositivos de protección y sus parámetros.
Los circuitos equivalentes dinámicos de los motores CC están representados en la Figura 5.12. El voltaje de la fuente v Corriente del refuerzo del motor IA y RETRACT EMF se designa mediante letras en la parte inferior del caso para enfatizar que estos son valores instantáneos de cantidades variables de tiempo.
B y J son respectivamente el coeficiente de fricción viscosa en NM / RAD / SEC y el momento polar de inercia en Kg-M2 del sistema del motor del motor mencionado en el eje del motor.

La ecuación de voltaje del circuito de refuerzo de transición viene dada por

Dinámica del sistema de carga del motor

Más
![]()
El análisis de transición anterior del motor DC es válido para cualquier motor de CC. En el caso de un motor excitado por separado cuando la corriente de campo se mantiene constante, el flujo permanece constante y (5.16) y (5.17) son ecuaciones diferenciales lineales.
En el caso de un motor en serie, debido a la saturación del circuito magnético, el flujo es una función no lineal de la corriente de refuerzo y, en consecuencia, (5.16) y (5.17) son ecuaciones diferenciales no lineales.
Incluso si el circuito magnético es supuestamente lineal descuidando la saturación, (5.16) y (5.17) son ecuaciones diferenciales no lineales debido a que E es proporcional al producto de IA y ωm, y T son proporcionales a I2A.
Por lo tanto, para una serie en serie, estas ecuaciones no se pueden resolver digitalmente utilizando el método RungeKutta de 4to orden o el método del corrector predictor.
Análisis de transición del motor excitado por separado con control inusual:
Cuando la corriente de campo se mantiene constante, el flujo permanece constante. Reemplazo de Keφ con una constante K en las ecuaciones. (5.16) a (5.18), da

Diferenciar la ecuación. (5.20) da
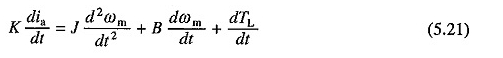
Sustitución en la ecuación. (5.19) para DIA / DT de (5.21) y reordenamiento Los términos dan
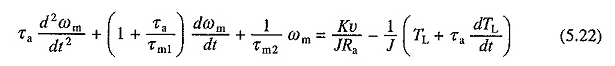
Diferenciar la ecuación. (5.19) da

Sustitución en la ecuación. (5.20) para dωm / dt de la ecuación. (5.23) y reorganizar los términos
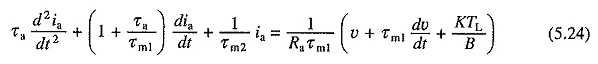
O


Las ecuaciones (5.22) y (5.24) son ecuaciones diferenciales lineales de la segunda tasa y se pueden resolver si se conocen las condiciones iniciales apropiadas. Una vez que la relación IA vs t se obtiene de la ecuación. (5.24), se puede calcular la relación t vs t.
Análisis de transición del inicio del motor excitado por separado con el control del refuerzo:
Aquí se considerará un análisis de transición del proceso de inicio para demostrar cómo se utilizan las ecuaciones mencionadas anteriormente.
Se supondrá que el motor se inicia con un voltaje V constante impresionado a través de sus terminales contra un torque de carga constante TL y con una RA de resistencia fija en su circuito de refuerzo.
Es habitual suponer que el motor solo comienza después de que su par desarrollado excede el par de carga. Porque esta corriente del motor debe alcanzar el valor que le dio

Cuando el motor está conectado a la fuente de alimentación, el valor inicial de la corriente es cero y debido a la inductancia del circuito inusual, lleva un cierto tiempo alcanzar el valor.
Durante todo este período, que se calificará como el primer intervalo de la respuesta de transición, el motor permanece en una parada y, por lo tanto, su EMF trasero sigue siendo cero. El motor se comporta como una RA simple: la carga. Por lo tanto, su corriente está dada por

El segundo intervalo de respuesta transitoria comienza después de que la corriente alcanza el valor. Dado que V y TL son constantes, DV / DT y DTL / DT serán cero. Sustituyendo estos valores en las ecuaciones. (5.22) y (5.24) da
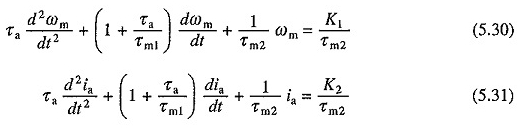
O
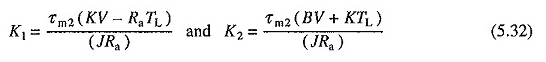
K1 y K2 representan los valores permanentes de velocidad y corriente de corriente con un par de carga igual a TL.
Condiciones iniciales necesarias para la solución de ecuaciones. (5.30) y (5.31) son
![]()
Dado que al comienzo de este intervalo, el par motor es igual al par de carga, de la ecuación. (5.17)

Más lejos de la ecuación. (5.16)

Soluciones iguales. (5.30) y (5.31) con las condiciones iniciales dadas por (5.33) a (5.35), tendrán el formulario:

donde α1 y α2 son raíces de ecuaciones características y están dadas por
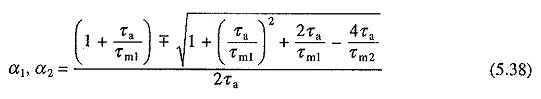
Tenga en cuenta que las ecuaciones anteriores se derivaron midiendo el tiempo al comienzo del segundo intervalo.
Para motores de menos de 1000 kW, las raíces α1 y α2 son generalmente reales.
Para motores de tamaño más grande y mediano, con una inductancia externa conectada en el circuito de refuerzo, como en el caso de un helicóptero y un análisis de transición suministrado por un motor de CC, las raíces pueden ser complejas.
La naturaleza de las curvas ωm vs t e ia vs t para los transitorios iniciales, cuando las raíces son reales, se representan en la Figura 5.13 (a).
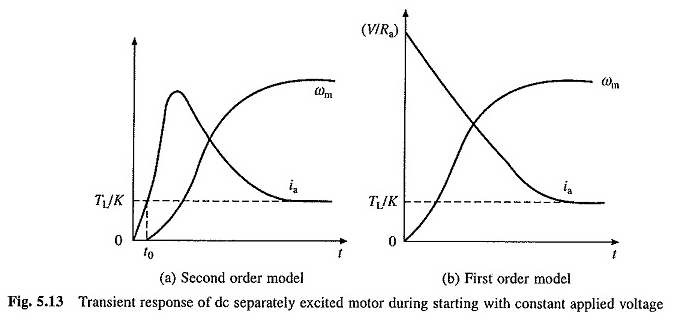
En motores pequeños, τa es muy pequeño debido a una gran resistencia al devanado del refuerzo. Por lo tanto, se puede pasar por alto. Sustituyendo τa = 0 en las ecuaciones. (5.30) y (5.31) da
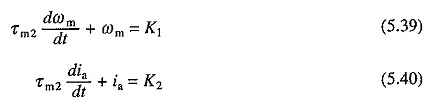
De τa = 0, la corriente va al valor V / ra en tiempo cero. Por lo tanto, las condiciones iniciales son
![]()
Soluciones iguales. (5.39) y (5.40) rendimiento

La naturaleza de ωm con respecto a las curvas T y AI en comparación con estas ecuaciones se representa en la Figura 5.13 (6).
Análisis de transición del frenado dinámico del motor excitado por separado:
Se supone que una carga activa TL constante está actuando en el eje del motor. La velocidad de transición y las ecuaciones de corriente se pueden obtener sustituyendo un nuevo valor por la resistencia del circuito inusual y v = 0 en las ecuaciones. (5.30) y (5.31). Dio

Aquí también: K3 y K4 representan respectivamente los valores de velocidad y corriente en el estado de equilibrio. Esta operación permanente ocurrirá cuando el par de carga TL activo esté autorizado para conducir el motor en la dirección opuesta. Las condiciones iniciales necesarias para la solución de estas ecuaciones se obtienen de la siguiente manera:
Se supone que en el inicio del frenado, el motor funcionó en el estado de equilibrio con un par de carga TL. Luego de la ecuación. (5.30)
![]()
Para un caso general, K1 debe considerarse la velocidad inicial.
El frenado se puede aplicar con o sin abrir el circuito de refuerzo. Cuando no está abierto, cuando el automóvil se hace pasar al frenado, se mantendrá la continuidad de la corriente de refuerzo, entonces el valor inicial de la corriente, de la ecuación. (5.31), será K2.
Sin embargo, si está abierto, el valor inicial de la corriente será cero. Aquí, suponemos que está abierto durante la transición. ENTONCES
![]()
Ahora de las ecuaciones. (5.19) y (5.20), sustituyendo v = 0, ia = 0 y ωm = k1.
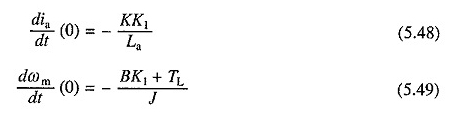
Soluciones iguales. (5.43) y (5.44) con las condiciones iniciales de (5.46) a (5.49) tendrán el formulario:
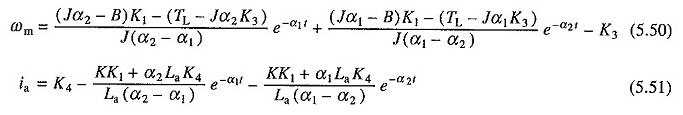
donde α1 y α2 están dados por la ecuación. (5.38).
La naturaleza de la respuesta transitoria en frenado dinámico para el caso de α1 y α2 reales se ilustra en la Figura 5.14.
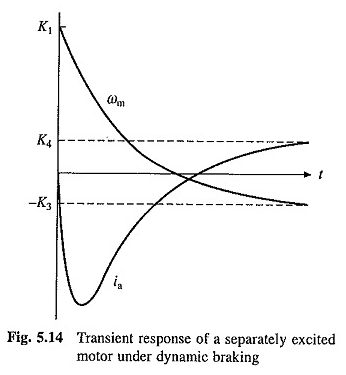
Las ecuaciones de transición de la operación de plug -in se obtienen de (5.19), (5.20), (5.22) y (5.24) sustitución – V por v.
Pérdidas de energía durante las operaciones de transición:
Las pérdidas de energía en el motor y en las resistencias en el circuito de refuerzo del motor, si existen, durante el período de funcionamiento transitorio, son necesarias para seleccionar las notas apropiadas del motor y la resistencia. También son necesarios para calcular la eficiencia y la eficiencia del proceso de transición.
Multiplica ambos lados de la ecuación. (5.16) por IA da

Dado que el par de fricción viscoso es parte del par de carga TL, tenemos una ecuación. (5.17)

Sustituyendo ecuaciones. (5.18) y (5.53) en (5.52) e integrando los dos lados de la ecuación resultante contra el rendimiento del tiempo
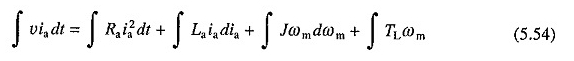
Esta ecuación estipula que en la energía total proporcionada por la fuente durante un proceso de transición, se desperdicia una parte en la resistencia del circuito de refuerzo, la segunda parte se almacena en la inductancia del circuito de refuerzo, la tercera parte se almacena en la inercia de las partes mecánicas y la carga se consume.
La energía almacenada en la inductancia del circuito de refuerzo es generalmente baja en comparación con otros términos de energía y, por lo tanto, se descuidará en el análisis posterior.
Comenzar el motor con un tensión V y TL de voltaje V y TL ahora se consideran ahora.
De

donde ωm0 es la velocidad ideal sin carga. Ecuaciones. (5.54) y (5.55)

La ecuación (5.56) da una expresión para la pérdida de energía en la resistencia del circuito de refuerzo de la máquina. Cuando se inicia sin carga, la velocidad final (estado de equilibrio) será Ωm0. Por lo tanto, la pérdida de energía en cualquier condición de carga E0 es

Es interesante observar que la pérdida de energía en el circuito de refuerzo del motor durante el arranque sin carga es igual a la energía cinética almacenada en las partes giratorias del motor a una velocidad de estado estable.
Además, es independiente de la duración del proceso de inicio, la naturaleza de la velocidad del pollo y las características de la corriente de velocidad del motor, el número de etapas de resistencia al arranque y el valor de la reister en cada paso.
Dado que ωm0 no será muy diferente de la velocidad en el estado de equilibrio con la carga TL en el eje del motor, el primer término en RHS de la ecuación. (5.56) Aproximadamente representa la pérdida de cobre durante el inicio, bajo cualquier carga y lo que se ha dicho sobre E0 también es aplicable a este término.
El segundo término depende de las características de la carga de carga de velocidad del motor y del valor de la resistencia inicial. Este término está representado por el área sombreada de la Figura 5.15.

Como se indicó anteriormente, el primer término en el lado derecho de (5.56) permanece sin cambios con el cambio en la resistencia inicial. Sin embargo, se puede reducir por un método de tensión de inicio reducido. Considere el caso en el que la tensión de la fuente se aplica en varios pasos iguales. La primera parte de la pérdida de cobre MTH será
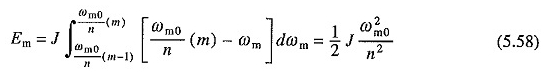
Dado que esta parte de la pérdida de cobre será la misma en todas las n pasos, no se convierte en un total de pérdida de cobre durante el inicio

Comparación de esto con la ecuación. (5.57) muestra que la pérdida de cobre sin carga se ha reducido por un factor de n.
Luego examinemos la pérdida durante el frenado reostático. Al sustituir V = 0, descuidándolo y suponiendo que el par de carga es constante e igual a TL, la siguiente ecuación puede derivarse de (5.52) y (5.53)
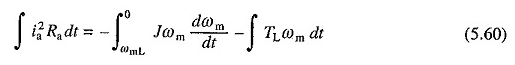
Se ha asumido que antes de frenar, el motor funcionaba en el estado de equilibrio contra un par de carga pasiva TL a una velocidad Ωml. En la integración de ecualización. (5.60) Renderizado

Esta ecuación indica que la carga absorbe parte de la energía cinética almacenada y que el resto se disipa en forma de pérdida de cobre.
Para obstruir, en la sustitución de —V por v y el = 0, en las ecuaciones. (5.52) y (5.53) se obtiene la siguiente ecuación para la pérdida de cobre
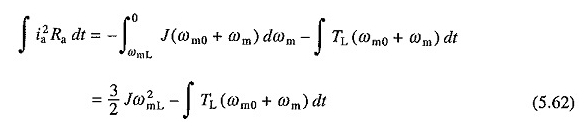
Ecuaciones. (5.61) y (5.62) las pérdidas de cobre sin carga bajo frenado y enchufe dinámico serán 1/2 JΩ20 y 3/2 JΩ20 respectivamente. Por lo tanto, la pérdida durante la conexión será tres veces esto durante el frenado dinámico.
Dado que durante el enchufe en la energía obtenida de la energía cinética de las piezas rotativas es de solo 1/2 jΩ2m0, el resto Jω2m0 se toma de la fuente de alimentación.
Análisis de transición del motor excitado por separado con control de campo:
O la tensión de refuerzo constante. AHORA
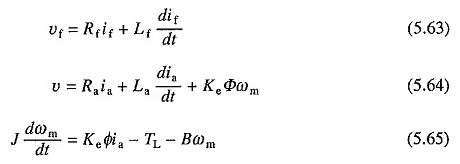
Aquí φ es una función no lineal de IF. Si se descuida la saturación y se supone que φ es proporcional a SO (5.64) y (5.65) se puede escribir como

donde k ′ = kekφ.
Debido a los términos k′ifωm y k′ifia, que implican el producto de dos variables (5.66) y (5.67) son ecuaciones no lineales, incluso si se ha descuidado la saturación.
Por lo tanto, este análisis se puede llevar a cabo utilizando métodos digitales para resolver ecuaciones diferenciales no lineales, como el 4to Runege-Kutta y los métodos predictivos.
Un caso especial con el control de la tierra ocurre cuando la corriente de refuerzo se mantiene constante. Luego, la ecuación describe la dinámica del sistema de carga del motor. (5.63) con la siguiente ecuación:

donde ka = kekφia e ia es la corriente de refuerzo.
De la ecuación. (5.68) Se puede obtener la expresión de IF y DIF / DT. Reemplácelos en la ecuación. (5.63) y reorganizar los «términos dan

O

El motor se puede analizar para su respuesta de transición utilizando la ecuación. (5.69) siempre que se conozcan las condiciones iniciales. El valor inicial de ωm se conocerá desde el punto de operación hasta el estado de equilibrio inmediatamente antes de los transitorios y el valor inicial de DΩM / DT se calcula a partir de la ecuación. (5.68).

