Control de circuito cerrado del motor CC:
Control de circuito cerrado del motor CC: el comportamiento dinámico de un sistema se describe mediante un conjunto de ecuaciones diferenciales. En numerosas ocasiones, la solución de estas ecuaciones requiere la evaluación de las integrales de convolución, lo que puede ser una tarea difícil.
En tales casos, un análisis más simple se hace factible mediante el uso de funciones de transferencia utilizando transformaciones de Laplace.
Se define una función de transferencia para sistemas invariantes lineales, como la relación de la transformación de Laplace de la variable de salida en la transformación de la variable de entrada, suponiendo que todas las condiciones iniciales son cero.
Los sistemas no lineales con uno o más parámetros varían el tiempo no pueden tener funciones de transferencia porque la transformación de Laplace no existe para ellos. Sin embargo, los sistemas de capacitación con no lentes pueden ser linealizados y se pueden aplicar la teoría de retroalimentación lineal.
Estos sistemas pueden estar representados por diagramas de bloques o gráficos de flujo de señal. En el enfoque del diagrama de bloques, un bloque representa la función de un componente con su entrada y su salida. La función de transferencia de componentes está escrita en el bloque. Por lo tanto, la función de transferencia es de la forma
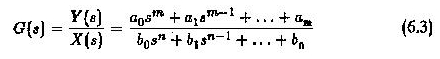
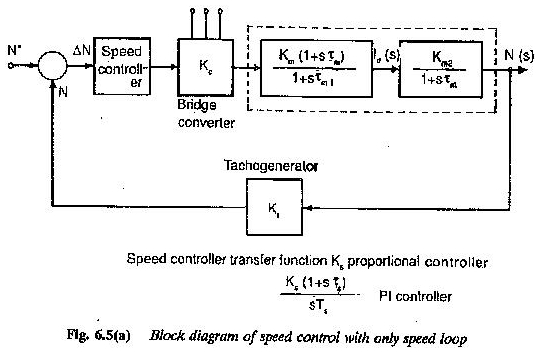
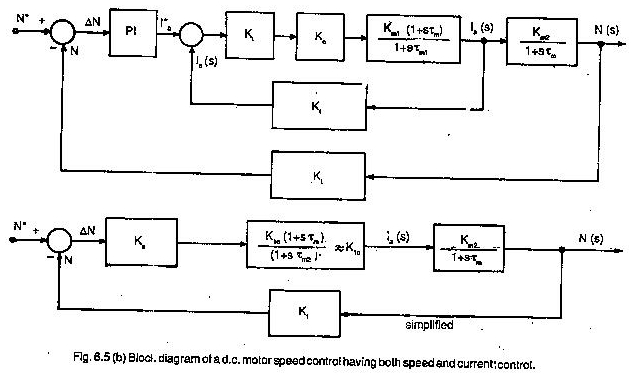
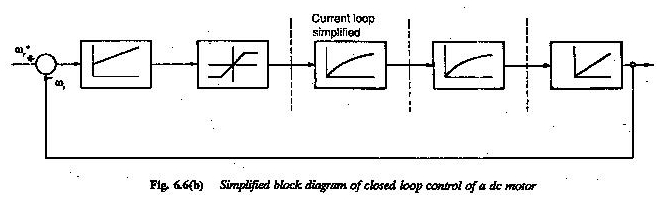
Al definir la función de transferencia, la transformación de Laplace se ha utilizado porque transforma todas las ecuaciones diferenciales en ecuaciones algebraicas simples. La Figura 6.5 representa un diagrama de bloques de un motor de CC en un sistema de accionamiento.
El motor tiene un voltaje de refuerzo como variable de entrada y velocidad como variable de salida. La función de transferencia está escrita en el bloque.
La función de transferencia se deriva de todas las ecuaciones diferenciales que describen el comportamiento del sistema. Sin embargo, no se refiere a la estructura física interna del sistema.
Los diferentes sistemas físicos pueden tener funciones de transferencia similares y también un comportamiento dinámico similar. La función de transferencia está en términos de parámetros del sistema y es una propiedad del sistema. No depende de la magnitud o la naturaleza de la entrada. La mayor potencia de S en el denominador representa el orden del sistema.
Se da un ejemplo simple en lo que sigue para mostrar la simplicidad que ofrece las funciones de transferencia.
Ejemplo:
Dos circuitos RC están conectados en la cascada, como se muestra en la Figura 6.6.
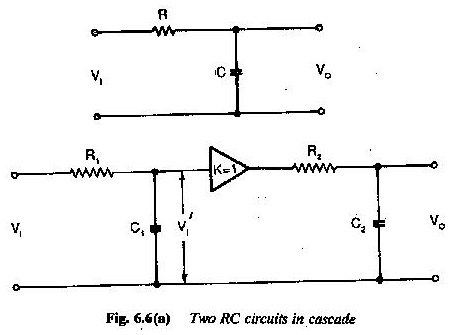
La entrada es un paso
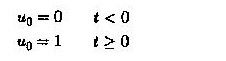El amplificador se usa para operar como un acoplamiento CC entre ellos. Determine la variación temporal de U2. Sabemos
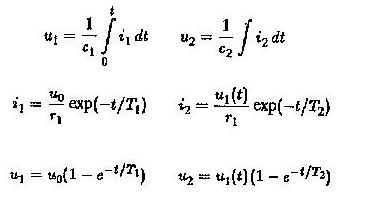
La relación U2 / UO se obtiene evaluando la integral de la convolución
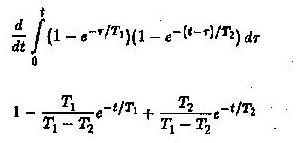
Si se agrega un circuito RC más en cascada al circuito dado: la evaluación de U2 / U0 es muy difícil.
Por otro lado, si se utiliza el enfoque de la función de transferencia, tenemos
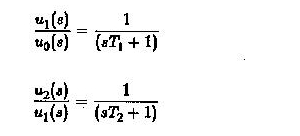
Al usar estas ecuaciones, tenemos
puede evaluarse muy fácilmente
como usando una expansión de fracción parcial.