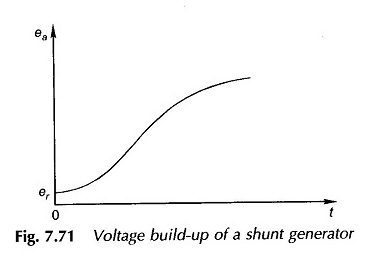
Motor CC excitado por separado para el análisis dinámico:
El motor CC excitado por separado para el análisis dinámico: las máquinas CC son bastante versátiles y pueden dar una variedad de características VA y a la velocidad de velocidad mediante combinaciones apropiadas de varios devanados de campo.
Motor cc paralelo
Con los controles de semiconductores, sus velocidades y salidas se pueden controlar fácilmente en un amplio rango para una dieta dinámica y permanente. Al agregar el circuito de retroalimentación, las características de la máquina aún se pueden modificar. El propósito de esta sección es estudiar máquinas DC en referencia a sus características dinámicas.
Para ilustración, considere la máquina CC excitada representada por separado esquemáticamente en la Figura 7.68. Para facilitar el análisis, se realizan las siguientes hipótesis:
- El eje del marco MMF se fija en el espacio, a lo largo del eje Q.
- Se descuida el efecto de desmagnetización de la reacción interijack.
- Se supone que el circuito magnético es lineal (sin histéresis y saturación). En consecuencia, todas las inductancias (que entraron en juego en el análisis dinámico) se consideran constantes.
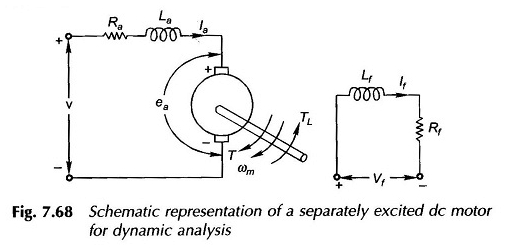
Los dos parámetros de inductancia que aparecen en la Figura 7.68 se definen a continuación:
- La = auto-inductancia del refuerzo causado por el flujo de refuerzo; Esto es bastante pequeño y puede descuidarse sin provocar un error grave en el análisis dinámico
- Lf = autoinducción del devanado de campo; Es lo suficientemente grande para el campo de la derivación y debe tenerse en cuenta
Inductancia mutua (entre campo y refuerzo) = 0; Porque los dos están en cuadratura espacial.
Además, para el motor CC excitado por separado para un análisis dinámico, es práctico usar la velocidad RAD / S en lugar de las RPM.
Aplicar la ley de Kirchhoff al circuito de refuerzo,
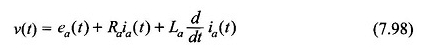
O
![]()
Lo mismo para el circuito de campo,
![]()
Para el funcionamiento del automóvil, el motor CC excita por separado para un análisis dinámico para el sistema mecánico es

O
J = Momento de inercia del motor y carga en NMS2
D = coeficiente de amortiguación de viscos que representa una pérdida de par de torque, nm rad / s
El almacenamiento de energía se asocia con campos magnéticos producidos por IF y AI y con la energía cinética de las piezas rotativas. Las ecuaciones anteriores son un conjunto de ecuaciones de estado no lineales (debido a productos si (t) ωm e if (t) ia (t) con variables de estado si, ia y Ωm. La solución debe obtenerse digitalmente.
Funciones de transferencia y diagrama de bloques del motor CC excitado por separado:
En el caso lineal lineal único de la respuesta del motor a los cambios en el voltaje de inicio, se supone que el voltaje de campo es constante y que el estado de equilibrio existe en el circuito de campo, es decir, si = constante. Las ecuaciones (7.98), (7,100) y (7.101) ahora se vuelven lineales como se indica a continuación

EQS de transformación de Laplace (7.102) y (7.103),
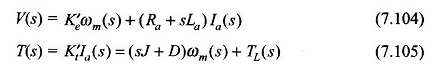
Estas ecuaciones pueden reorganizarse como 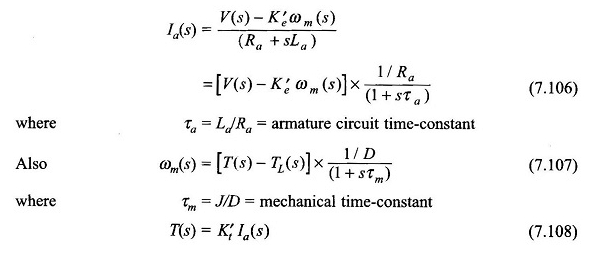
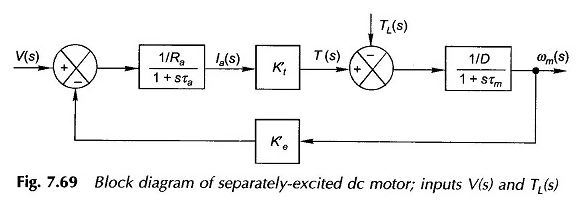
De las ecuaciones (7.106) – (7.108), el diagrama de bloques del motor se puede dibujar como en la Figura 7.69. Es un sistema de retroalimentación de segundo precio con una respuesta oscilatoria en general. Se reduce a un sistema simple de primer grado, si y, por lo tanto, τa se descuida.
Acumulación de tensión del generador de derivación:
Ya se ha discutido la explicación cualitativa del proceso de acumulación de tensión en un generador de derivación. Aquí, se dará el tratamiento matemático de este problema, lo que de hecho se reduce a la solución de una ecuación diferencial no lineal.
Refiriéndose a la Fig. 7.70, vemos que para cualquier corriente de campo, la intercepción AB, entre la línea OCC y RF da la caída de voltaje causada por la tasa de cambio de φF y la intercepción BC da la caída de resistencia al campo. Los dos balances que el EMF generó EA (descuidando IFRA, la caída del refuerzo) juntos. Entonces 
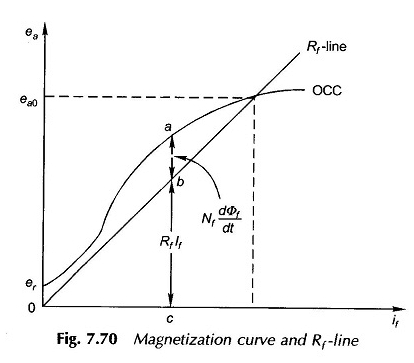
El flujo de campo φF es más alto que el flujo de aire de aire del eje directo φD debido a la fuga.
Teniendo en cuenta

Aquí, σ se conoce como el coeficiente de dispersión.
Recordando la ecuación. (7.3),


Sustituyendo las ecuaciones (7.110) y (7.111) en la ecuación. (7.109),

Multiplica el numerador y el denominador por NFPAG
O
Pag es la permeabilidad de la caminata aérea / posterior 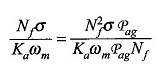
Se reconoce fácilmente que el numerador es el valor insaturado de la inductancia de campo, LF, y el denominador es la pendiente de la línea de ojo de aire. Ambas son constantes. Entonces, 
Esta integral se puede evaluar gráficamente resumiendo las áreas en una ruta 1 / (EA – RF IF) contra EA. Este enfoque se utiliza para trazar EA contra el tiempo.
El tiempo teórico necesario para que el EMF generado alcance el valor del vacío, EA0 sería infinito; Por lo tanto, en la práctica, se toma el tiempo requerido para alcanzar 0.95 EA0 como el tiempo necesario para llegar a EA0. La variación de la EA a lo largo del tiempo se dibuja en la Figura 7.71.
La respuesta es bastante lenta porque solo las pequeñas diferencias de voltaje (= EA – RFIF) contribuyen a la acumulación de flujos (φF).