Analisi del motore CC di transizione:
L’avvio, la frenata, il cambiamento di velocità e il cambiamento di carico sono l’analisi transitoria del motore di corrente continua che si verifica comunemente in un giocatore industriale.
Uno è interessato a sapere come la corrente, la coppia e la velocità del motore di guida cambiano nel tempo in queste operazioni di transizione.
Uno è anche interessato a conoscere le perdite di energia, in particolare quelli responsabili del riscaldamento del motore e del tempo impiegato per il completamento dell’analisi transitoria del motore DC.
Queste informazioni sono necessarie da parte del progettista per selezionare una notazione appropriata del motore, la natura e il tipo di apparecchiatura di controllo e il suo calendario operativo e i tipi di dispositivi di protezione e i loro parametri.
I circuiti equivalenti dinamici dei motori CC sono rappresentati nella Figura 5.12. La corrente di tensione di origine V della IA e il rinforzo del motore EMF di ritratto sono designati da lettere nella parte inferiore del caso per sottolineare che si tratta di valori istantanei di quantità di tempo variabili.
B e J sono rispettivamente il coefficiente di attrito viscoso in NM / rad / sec e il momento polare di inerzia in kg-m2 del sistema motorio del motore menzionato sull’albero del motore.

L’equazione di tensione del circuito di rinforzo transitorio è data

Dinamica del sistema di carico del motore

Ulteriore
![]()
L’analisi di transizione di cui sopra del motore CC è valida per qualsiasi motore CC. In caso di un motore eccitato separatamente quando la corrente di campo è mantenuta costante, il flusso rimane costante e (5.16) e (5.17) sono equazioni differenziali lineari.
Nel caso di un motore in serie, a causa della saturazione del circuito magnetico, il flusso è una funzione non lineare della corrente di rinforzo e, di conseguenza, (5.16) e (5.17) sono equazioni differenziali non lineari.
Anche se il circuito magnetico è presumibilmente lineare trascurando la saturazione, (5.16) e (5.17) sono equazioni differenziali non lineari dovute a essere proporzionali al prodotto di IA e ωm e sono proporzionali a I2A.
Pertanto, per una serie in serie, queste equazioni non possono essere risolte digitalmente utilizzando il metodo Rungekutta del 4 ° ordine o il metodo correttore predittore.
Analisi di transizione del motore eccitato separatamente con un controllo insolito:
Quando la corrente di campo viene mantenuta costante, il flusso rimane costante. Sostituzione Keφ con una K costante nelle equazioni. (Da 5,16) a (5.18), dà

Differenziando l’equazione. (5.20) dà
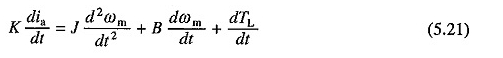
Sostituendo nell’equazione. (5.19) per dia / dt di (5.21) e riarrangiamento che i termini danno
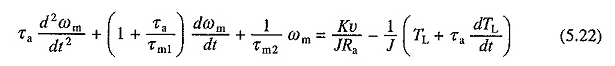
Differenziando l’equazione. (5.19) dà

Sostituendo nell’equazione. (5.20) per dωm / dt dell’equazione. (5.23) e riorganizzare i termini
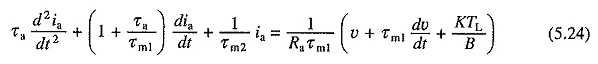
O


Le equazioni (5.22) e (5.24) sono equazioni differenziali lineari di seconda rate e possono essere risolte se sono note le condizioni iniziali appropriate. Una volta ottenuta la relazione IA vs T dall’equazione. (5.24), la relazione t vs t può essere calcolata.
Analisi di transizione dell’inizio del motore eccitato separatamente con il controllo del rinforzo:
Un’analisi di transizione del processo di avvio sarà considerata qui per dimostrare come vengono utilizzate le equazioni sopra menzionate.
Si presume che il motore sia avviato con una tensione costante V colpita attraverso i suoi terminali contro una coppia di carica costante TL e con una RA di resistenza fissa nel suo circuito di rinforzo.
È normale supporre che il motore inizi solo dopo che la sua coppia sviluppata supera la coppia di ricarica. Perché questa corrente del motore dovrebbe raggiungere il valore dato da

Quando il motore è collegato all’alimentazione, il valore iniziale della corrente è zero e a causa dell’induttanza del circuito insolito, ci vuole un certo tempo per raggiungere il valore.
Durante questo intero periodo, che sarà qualificato come il primo intervallo della risposta di transizione, il motore rimane ad una fermata e quindi il suo EMF posteriore rimane zero. Il motore si comporta come un semplice RA – il carico. Pertanto la sua corrente è data da

Il secondo intervallo di risposta transitoria inizia dopo che la corrente raggiunge il valore esso. Poiché V e TL sono costanti, DV / DT e DTL / DT saranno zero. Sostituendo questi valori nelle equazioni. (5.22) e (5.24) danno
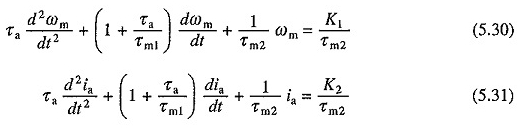
O
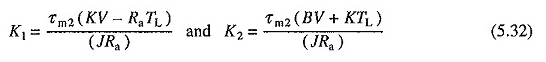
K1 e K2 rappresentano i valori permanenti di velocità e corrente di corrente con una coppia di carica pari a TL.
Condizioni iniziali necessarie per la soluzione delle equazioni. (5.30) e (5.31) sono
![]()
Dato che all’inizio di questo intervallo, la coppia del motore è uguale alla coppia di carico, dall’equazione. (5.17)

Più lontano dall’equazione. (5.16)

Uguali soluzioni. (5.30) e (5.31) con le condizioni iniziali fornite da (da 5,33) a (5.35), avranno il modulo:

dove α1 e α2 sono radici di equazione caratteristica e sono dati da
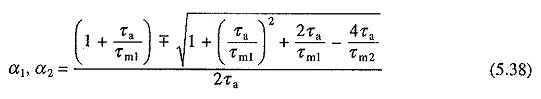
Si noti che le equazioni di cui sopra sono state derivate misurando il tempo all’inizio del secondo intervallo.
Per motori inferiori a 1000 kW, le radici α1 e α2 sono generalmente reali.
Per motori più grandi e di medie dimensioni, con un’induttanza esterna collegata nel circuito di rinforzo, come nel caso di un elicottero e un’analisi di transizione fornita da un motore a CC, le radici possono essere complesse.
La natura delle curve ωm vs t e ia vs t per i transitori start -up, quando le radici sono reali, sono rappresentate nella Figura 5.13 (a).
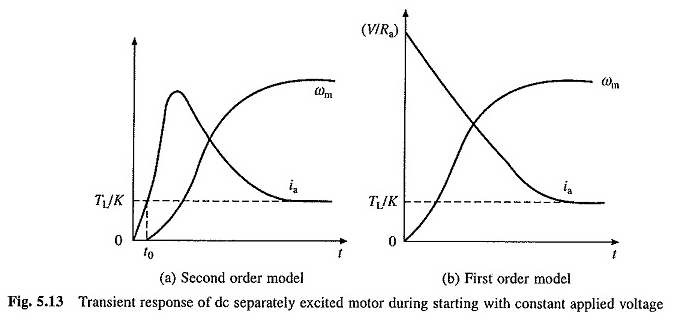
In piccoli motori, τa è molto piccolo a causa di una grande resistenza all’avvolgimento del rinforzo. Può quindi essere trascurato. Sostituendo τa = 0 nelle equazioni. (5.30) e (5.31) danno
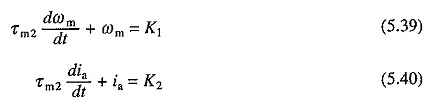
Da τa = 0, la corrente va al valore V / RA in tempo zero. Pertanto, le condizioni iniziali sono
![]()
Uguali soluzioni. (5.39) e (5.40) resa

La natura di ωm rispetto alle curve T e AI rispetto a queste equazioni è rappresentata nella Figura 5.13 (6).
Analisi di transizione della frenata dinamica del motore eccitato separatamente:
Si presume che un carico attivo TL costante agisca sull’albero del motore. La velocità di transizione e le equazioni di corrente possono essere ottenute sostituendo un nuovo valore per la resistenza del circuito insolito e V = 0 nelle equazioni. (5.30) e (5.31). Dà

Anche qui: K3 e K4 rappresentano rispettivamente i valori di velocità e corrente nello stato di equilibrio. Questo funzionamento permanente si verificherà quando la coppia di caricamento TL attivo è autorizzata a guidare il motore nella direzione opposta. Le condizioni iniziali necessarie per la soluzione di queste equazioni sono ottenute come segue:
Si presume che nell’inizio della frenata, il motore ha funzionato nello stato di equilibrio con una coppia di carico TL. Quindi dall’equazione. (5.30)
![]()
Per un caso generale, K1 deve essere considerato la velocità iniziale.
La frenata può essere applicata con o senza aprire il circuito di rinforzo. Quando non è aperto, quando l’automobile viene trasferita alla frenata, la continuità della corrente di rinforzo verrà mantenuta, quindi il valore iniziale della corrente, dall’equazione. (5.31), sarà K2.
Tuttavia, se è aperto, il valore iniziale della corrente sarà zero. Qui, supponiamo che sia aperto durante la transizione. COSÌ
![]()
Ora da Eqs. (5.19) e (5.20), sostituendo v = 0, ia = 0 e ωm = k1.
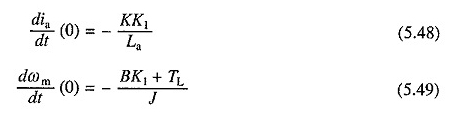
Uguali soluzioni. (5.43) e (5.44) con le condizioni iniziali da (5.46) a (5.49) avranno il modulo:
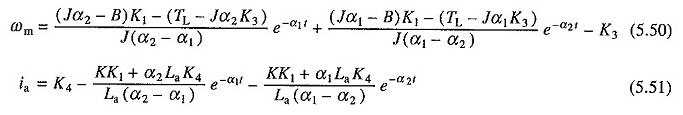
dove α1 e α2 sono somministrati dall’equazione. (5.38).
La natura della risposta transitoria sotto frenata dinamica per il caso di α1 e α2 reali è illustrata nella Figura 5.14.
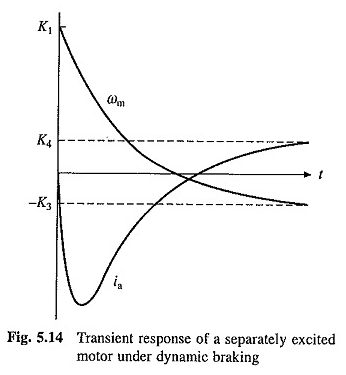
Le equazioni di transizione del funzionamento plug -in sono ottenute da (5.19), (5.20), (5.22) e (5.24) sostituendo – V per v.
Perdite di energia durante le operazioni di transizione:
Le perdite di energia nel motore e nei resistori nel circuito di rinforzo del motore, se vi sono, durante il periodo operativo transitorio, sono necessarie per selezionare le note appropriate del motore e della resistenza. Sono anche necessari per calcolare l’efficienza e l’efficienza del processo di transizione.
Moltiplicare entrambi i lati dell’equazione. (5.16) di IA dà

Poiché la coppia di attrito viscoso fa parte della coppia di carico TL, abbiamo l’equazione. (5.17)

Sostituzione delle equazioni. (5.18) e (5.53) in (5.52) e integrazione dei due lati dell’equazione risultante dal rendimento del tempo
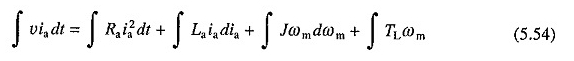
Questa equazione stabilisce che sull’energia totale fornita dalla sorgente durante un processo di transizione, viene sprecata una parte nella resistenza del circuito di rinforzo, la seconda porzione viene immagazzinata nell’induttanza del circuito di rinforzo, la terza porzione viene immagazzinata nell’inerzia delle parti meccaniche e il resto è consumato dal carico.
L’energia immagazzinata nell’induttanza del circuito di rinforzo è generalmente bassa rispetto ad altri termini energetici e sarà quindi trascurata nell’analisi successiva.
L’avvio del motore con una tensione V e una coppia di ricarica TL costante ora sono ora considerati.
Da

dove ωm0 è la velocità ideale senza carico. Equazioni. (5,54) e (5,55)

L’equazione (5.56) fornisce un’espressione per la perdita di energia nella resistenza del circuito di rinforzo della macchina. Quando è iniziata senza carico, la velocità finale (stato di equilibrio) sarà ωm0. Pertanto, la perdita di energia in qualsiasi condizione di carico E0 è

È interessante notare che la perdita di energia nel circuito di rinforzo del motore durante l’avvio senza carico è uguale all’energia cinetica immagazzinata nelle parti rotanti del motore a una velocità statale stabile.
Inoltre, è indipendente dalla durata del processo di partenza, dalla natura della velocità del pulcino e dalle caratteristiche della corrente di velocità del motore, dal numero di fasi della resistenza di avvio e dal valore della reister in ogni fase.
Poiché ωm0 non sarà molto diverso dalla velocità nello stato di equilibrio con il carico TL sull’albero del motore, il primo termine su RHS dell’equazione. (5.56) rappresenta approssimativamente la perdita di rame durante l’inizio -up sotto qualsiasi carico e ciò che è stato detto su E0 è applicabile anche a questo termine.
Il secondo termine dipende dalle caratteristiche del carico di velocità del motore e dal valore della resistenza iniziale. Questo termine è rappresentato dall’area ombreggiata della Figura 5.15.

Come indicato sopra, il primo termine sul lato destro di (5,56) rimane invariato con il cambiamento nella resistenza iniziale. Tuttavia, può essere abbassato con un metodo di tensione di avvio ridotto. Considera il caso in cui la tensione di origine viene applicata in una serie di passaggi uguali. La prima parte della perdita di rame MTH sarà
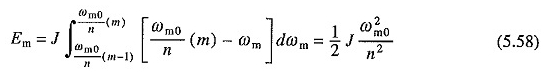
Poiché questa parte della perdita di rame sarà la stessa su tutte le n passaggi, non è perdita totale di rame durante l’inizio

Confronto di questo con l’equazione. (5.57) mostra che la perdita di rame senza carico è stata ridotta di un fattore di n.
Esaminiamo quindi la perdita durante la frenata reostatica. Sostituendo v = 0, trascurandolo e supponendo che la coppia di carico sia costante e uguale a TL, la seguente equazione può essere derivata da (5.52) e (5.53)
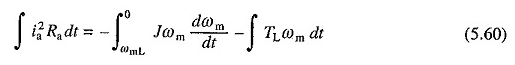
È stato ipotizzato che prima della frenata, il motore operava nello stato di equilibrio contro una coppia di carica passiva TL a una velocità di ωml. Sull’integrazione EQ. (5.60) reso

Questa equazione indica che il carico assorbe parte dell’energia cinetica immagazzinata e che il resto viene dissipato sotto forma di perdita di rame.
Per intasamento, sulla sostituzione di —V per v e il = 0, nelle equazioni. (5.52) e (5.53) si ottiene la seguente equazione per la perdita di rame
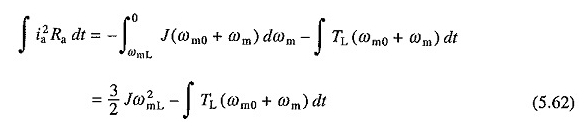
Equazioni. (5.61) e (5.62) le perdite di rame senza carico in frenata e tappo dinamico saranno rispettivamente 1/2 jω20 e 3/2 jω20. Pertanto, la perdita durante la connessione sarà tre volte questa durante la frenata dinamica.
Dato che durante l’energia della spina ottenuta dall’energia cinetica dei pezzi rotanti è solo 1/2 jω2m0, il resto jω2m0 viene preso dall’alimentazione.
Analisi di transizione del motore eccitato separatamente con il controllo del campo:
O la costante tensione di rinforzo. ORA
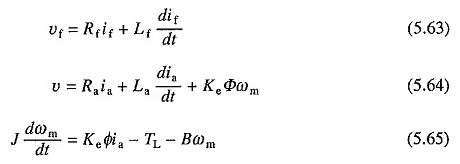
Qui φ è una funzione non lineare di IF. Se la saturazione viene trascurata e φ dovrebbe essere proporzionale a SO (5.64) e (5.65) può essere scritto come

dove k ′ = kekφ.
A causa dei termini K′IFωm e K′IFIA, che coinvolgono il prodotto di due variabili (5.66) e (5.67) sono equazioni non lineari, anche se la saturazione è stata trascurata.
Pertanto, questa analisi può essere effettuata utilizzando metodi digitali per risolvere equazioni differenziali non lineari come il 4 ° Runege-Kutta e i metodi predittivi.
Un caso speciale con il controllo del suolo si verifica quando la corrente di rinforzo viene mantenuta costante. Quindi, la dinamica del sistema di carico del motore è descritta dall’equazione. (5.63) con la seguente equazione:

dove ka = kekφia e ia è la corrente del rinforzo.
Dell’equazione. (5.68) L’espressione di IF e DIF / DT può essere ottenuta. Sostituili nell’equazione. (5.63) e riorganizzare i “Termini danno

O

Il motore può essere analizzato per la sua risposta di transizione usando l’equazione. (5.69) a condizione che siano note le condizioni iniziali. Il valore iniziale di ωm sarà noto dal punto operativo allo stato di equilibrio immediatamente prima dei transitori e il valore iniziale di dωm / dt viene calcolato dall’equazione. (5.68).

