Controllo a circuito chiuso del motore CC:
Controllo a circuito chiuso del motore CC – Il comportamento dinamico di un sistema è descritto da una serie di equazioni differenziali. In numerose occasioni, la soluzione di queste equazioni richiede la valutazione degli integrali della convoluzione che può essere un compito difficile.
Schema a blocchi motore cc
In tali casi, un’analisi più semplice è resa possibile utilizzando le funzioni di trasferimento usando le trasformazioni di Laplace.
Una funzione di trasferimento è definita per sistemi invarianti lineari come il rapporto tra la trasformazione di Laplace della variabile di output in trasformazione della variabile di input, supponendo che tutte le condizioni iniziali siano zero.
I sistemi non lineari con uno o più parametri che variano il tempo non possono avere funzioni di trasferimento perché la trasformazione di Laplace non esiste per loro. Tuttavia, i sistemi di formazione con non leies possono essere linearizzati e è possibile applicare la teoria del feedback lineare.
Questi sistemi possono essere rappresentati da diagrammi a blocchi o grafici a flusso di segnale. Nell’approccio del diagramma a blocchi, un blocco rappresenta la funzione di un componente con il suo input e il suo output. La funzione di trasferimento dei componenti è scritta nel blocco. Pertanto, la funzione di trasferimento è della forma
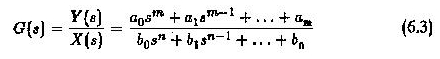
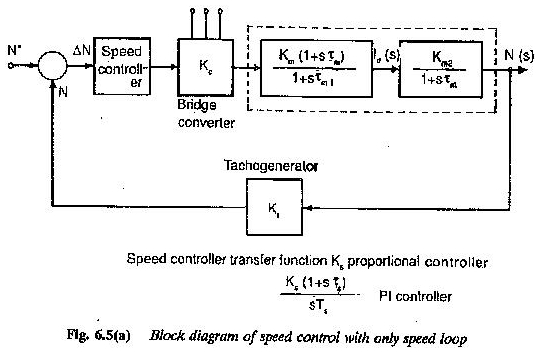
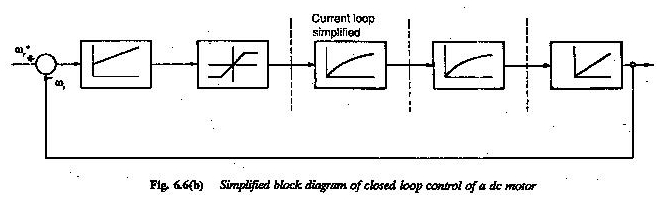
Durante la definizione della funzione di trasferimento, la trasformazione di Laplace è stata utilizzata perché trasforma tutte le equazioni differenziali in semplici equazioni algebriche. La Figura 6.5 rappresenta uno schema a blocchi di un motore a CC in un sistema di azionamento.
Il motore ha una tensione di rinforzo come variabile di ingresso e velocità come variabile di uscita. La funzione di trasferimento è scritta nel blocco.
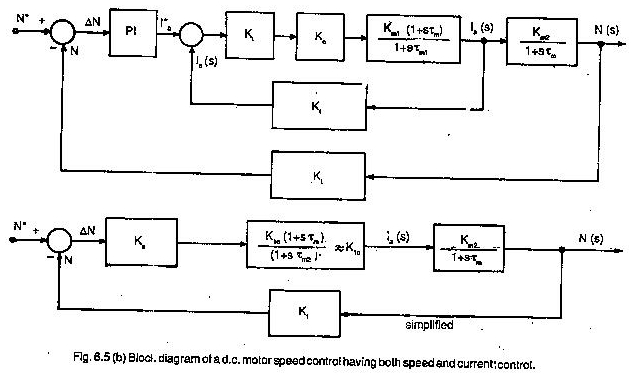
La funzione di trasferimento deriva da tutte le equazioni differenziali che descrivono il comportamento del sistema. Tuttavia, non riguarda la struttura fisica interna del sistema.
Diversi sistemi fisici possono avere funzioni di trasferimento simili e anche comportamenti dinamici simili. La funzione di trasferimento è in termini di parametri di sistema ed è una proprietà del sistema. Non dipende dalla grandezza o dalla natura dell’ingresso. La più alta potenza di S nel denominatore rappresenta l’ordine del sistema.
Un semplice esempio è fornito in ciò che segue per mostrare la semplicità offerta dalle funzioni di trasferimento.
Esempio:
Due circuiti RC sono collegati in cascata, come mostrato nella Figura 6.6.
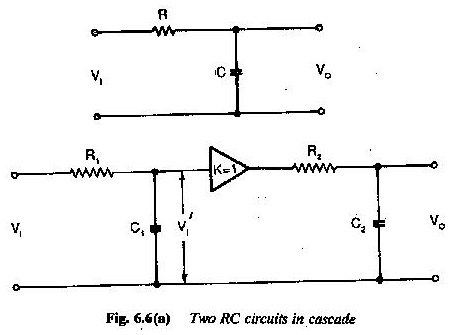
L’ingresso è un passaggio
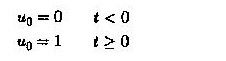 L’amplificatore viene utilizzato per funzionare come un accoppiamento CC tra di loro. Determina la variazione temporale di U2. Lo sappiamo
L’amplificatore viene utilizzato per funzionare come un accoppiamento CC tra di loro. Determina la variazione temporale di U2. Lo sappiamo
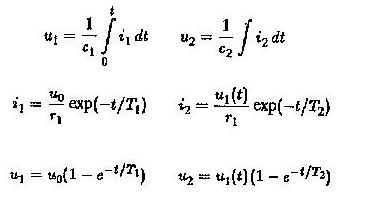
Il rapporto U2 / UO è ottenuto valutando l’integrale della convoluzione
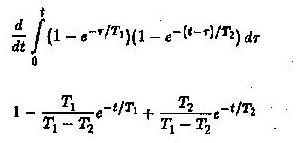
Se un altro circuito RC viene aggiunto in cascata al circuito dato – la valutazione di U2 / U0 è molto difficile.
D’altra parte, se viene utilizzato l’approccio della funzione di trasferimento
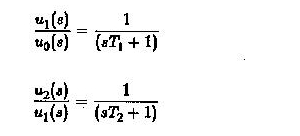
Usando queste equazioni, abbiamo

Può essere valutato molto facilmente

come usando un’espansione della frazione parziale.