Motore CC eccitato separatamente per analisi dinamica:
Il motore CC eccitato separatamente per l’analisi dinamica: le macchine CC sono piuttosto versatili e sono in grado di fornire una varietà di caratteristiche VA e alla velocità di velocità mediante combinazioni appropriate di vari avvolgimenti sul campo.
Con i controlli a semiconduttore, le loro velocità e uscite possono essere facilmente controllate su una vasta gamma per una dieta dinamica e permanente. Aggiungendo il circuito di feedback, le caratteristiche della macchina possono essere ancora modificate. Lo scopo di questa sezione è studiare le macchine DC in riferimento alle loro caratteristiche dinamiche.
Per illustrazione, considerare la macchina CC eccitata rappresentata separatamente nella Figura 7.68. Per facilitare l’analisi, vengono realizzate le seguenti ipotesi:
- L’asse del telaio MMF è fissato nello spazio, lungo l’asse Q.
- L’effetto smagnetizzante della reazione di InterIjack viene trascurato.
- Il circuito magnetico dovrebbe essere lineare (nessuna isteresi e saturazione). Di conseguenza, tutte le induttanze (che sono entrate in gioco nell’analisi dinamica) sono considerate costanti.
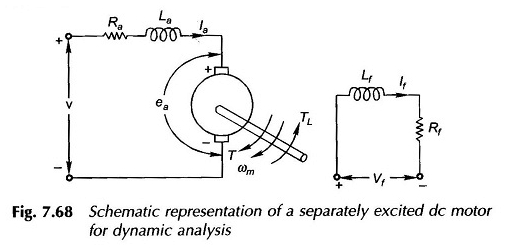
I due parametri di induttanza che compaiono nella Figura 7.68 sono definiti di seguito:
- La = autoinduttanza del rinforzo causato dal flusso di rinforzo; Questo è piuttosto piccolo e può essere trascurato senza provocare un grave errore nell’analisi dinamica
- LF = autoconduzione dell’avvolgimento del campo; È abbastanza grande per il campo di shunt e deve essere preso in considerazione
Induttanza reciproca (tra campo e rinforzo) = 0; Perché i due sono nella quadratura spaziale.
Inoltre, per il motore CC eccitato separatamente per un’analisi dinamica, è pratico utilizzare la velocità RAD / S anziché RPM.
Applicare la legge di Kirchhoff al circuito di rinforzo,
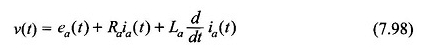
O
![]()
Lo stesso per il circuito di campo,
![]()
Per il funzionamento dell’automobile, il motore CC eccitato separatamente per un’analisi dinamica per il sistema meccanico è

O
J = momento di inerzia del motore e carico in NMS2
D = coefficiente di smorzamento visivo che rappresenta una perdita di coppia di coppia, NM RAD / S
Lo stoccaggio di energia è associato a campi magnetici prodotti da IF e AI e con l’energia cinetica dei pezzi rotanti. Le equazioni di cui sopra sono un insieme di equazioni di stato non lineari (a causa di prodotti se (t) ωm e se (t) ia (t) con variabili di stato se, ia e ωm. La soluzione deve essere ottenuta digitalmente.
Funzioni di trasferimento e diagramma a blocchi del motore CC eccitato separatamente:
Nel singolo caso lineare lineare della risposta del motore alle variazioni della tensione di inmarure, si presume che la tensione di campo sia costante e che lo stato di equilibrio esiste sul circuito di campo, vale a dire se = costante. Le equazioni (7,98), (7.100) e (7.101) ora diventano lineari come indicato di seguito

Laplace Transformation Eqs (7.102) e (7.103),
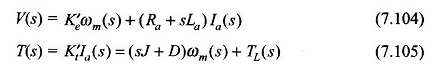
Queste equazioni possono essere riorganizzate come 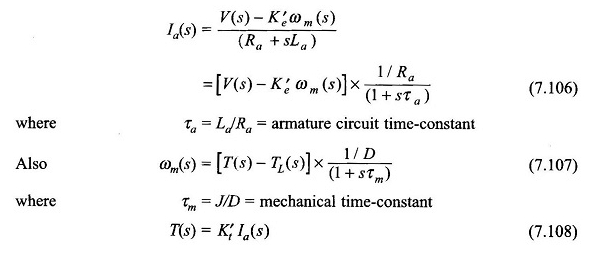
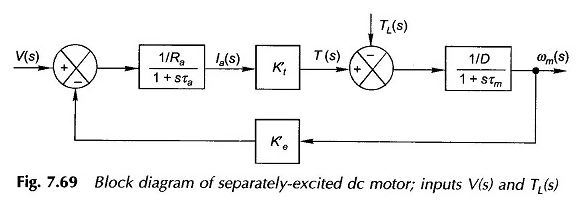
Dalle equazioni (7.106) – (7.108), il diagramma a blocchi del motore può essere disegnato come nella Figura 7.69. È un secondo sistema di feedback con una risposta oscillatoria in generale. Viene ridotto a un semplice sistema di primo rate, se e quindi τa viene trascurato.
Accumulo di tensione del generatore di shunt:
La spiegazione qualitativa del processo di accumulo di tensione in un generatore di shunt è già stata discussa. Qui verrà dato il trattamento matematico di questo problema, che in effetti si riduce alla soluzione di un’equazione differenziale non lineare.
Facendo riferimento alla Fig. 7.70, vediamo che per qualsiasi corrente di campo, l’intercettazione AB, tra l’OCC e la linea RF dà la caduta di tensione causata dalla velocità di variazione di φf e l’intercettazione BC dà la goccia nella resistenza al campo. I due equilibrano EMF generato EA (trascurando IFRA, la caduta del rinforzo) insieme. COSÌ 
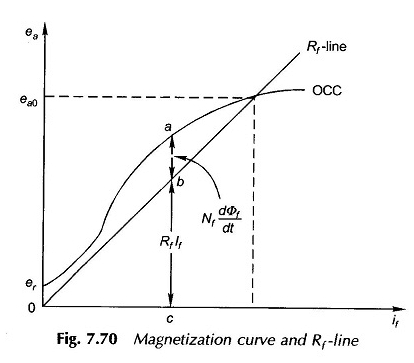
Il flusso di campo φf è superiore al flusso di gap d’aria dell’asse diretto φd a causa della perdita.
Tenendo conto

Qui, σ è noto come coefficiente di dispersione.
Ricordando l’Eq. (7.3),


Sostituire le equazioni (7.110) e (7.111) nell’equazione. (7.109),

Moltiplica il numeratore e il denominatore di NFPAG
O
PAG è la permeance di Air / Post Hike 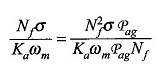
È facilmente riconosciuto che il numeratore è il valore insaturo dell’induttanza del campo, LF, e il denominatore è la pendenza della linea dell’aria. Entrambi sono costanti. COSÌ, 
Questo integrale può essere valutato graficamente riassumendo le aree su un percorso 1 / (ea – rf if) contro EA. Questo approccio viene utilizzato per tracciare EA contro il tempo.
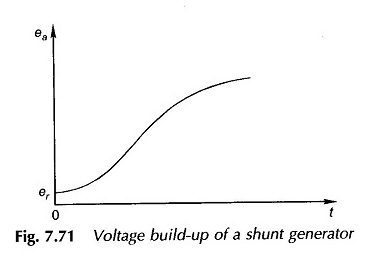
Il tempo teorico necessario per l’EMF generato per raggiungere il valore del vuoto, EA0 sarebbe infinito; Pertanto, in pratica, il tempo necessario per raggiungere lo 0,95 EA0 viene preso in quanto il tempo necessario per raggiungere EA0. La variazione dell’EA nel tempo è disegnata nella Figura 7.71.
La risposta è piuttosto lenta perché solo le differenze di tensione ridotta (= EA – RFIF) contribuiscono all’accumulo di flussi (φf).