CC Engine is afzonderlijk opgewonden voor dynamische analyse:
CC Engine is afzonderlijk opgewonden voor dynamische analyse – CC -machines zijn vrij veelzijdig en kunnen een verscheidenheid aan kenmerken geven VA en met de snelheidsnelheid door geschikte combinaties van verschillende veldwikkelingen.
Met halfgeleiderbesturing kunnen hun snelheden en uitgangen eenvoudig worden geregeld op een breed bereik voor dynamisch en permanent dieet. Door het feedbackcircuit toe te voegen, kunnen de kenmerken van de machine nog steeds worden gewijzigd. Het doel van deze sectie is om DC -machines te bestuderen in verwijzing naar hun dynamische kenmerken.
Overweeg ter illustratie de geëxciteerde CC -machine afzonderlijk weergegeven schematisch in figuur 7.68. Om de analyse te vergemakkelijken, worden de volgende hypothesen gemaakt:
- De as van het frame MMF is bevestigd in de ruimte, langs de as Q.
- Het demagneterende effect van de interijack -reactie wordt verwaarloosd.
- Het magnetische circuit wordt verondersteld lineair te zijn (geen hysterese en verzadiging). Bijgevolg worden alle inductanties (die in dynamische analyse in het spel kwamen) als constant beschouwd.
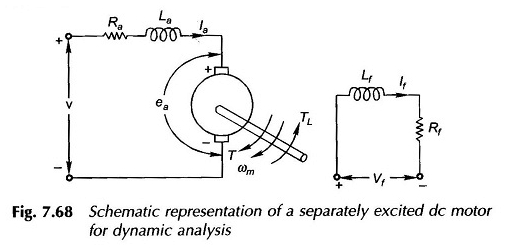
De twee inductieparameters die in figuur 7.68 verschijnen, worden hieronder gedefinieerd:
- De = zelfinductie van de versterking veroorzaakt door de versterkingsstroom; Dit is vrij klein en kan worden verwaarloosd zonder een ernstige fout in de dynamische analyse uit te lokken
- LF = zelfinductie van veldwikkeling; Het is groot genoeg voor het shuntveld en moet in aanmerking worden genomen
Wederzijdse inductantie (tussen veld en versterking) = 0; Omdat de twee in ruimte kwadratuur zijn.
Bovendien is het voor de geëxciteerde CC -motor afzonderlijk voor een dynamische analyse praktisch om RAD / S -snelheid te gebruiken in plaats van RPM.
Pas de wet van Kirchhoff toe op het versterkingscircuit,
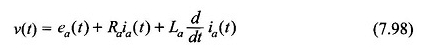
Of
![]()
Hetzelfde voor het veldcircuit,
![]()
Voor de werking van de auto is de CC -motor afzonderlijk opgewonden voor een dynamische analyse voor het mechanische systeem

Of
J = moment van motorbevestiging en belasting in NMS2
D = visque dempingcoëfficiënt die een verlies van koppelkoppel, NM rad / s vertegenwoordigt
Energieopslag wordt geassocieerd met magnetische velden geproduceerd door IF en AI en met de kinetische energie van roterende stukken. De bovenstaande vergelijkingen zijn een set niet-lineaire toestandsvergelijkingen (vanwege producten als (t) ωm en if (t) ia (t) met toestandsvariabelen als, ia en ωm. De oplossing moet digitaal worden verkregen.
Overdrachtsfuncties en motorblokdiagram CC CC afzonderlijk opgewonden:
In het enkele lineaire lineaire geval van de motorrespons op veranderingen in de maruurspanning, wordt aangenomen dat de veldspanning constant is en dat de evenwichtstoestand bestaat op het veldcircuit, dat wil zeggen als = constant. De vergelijkingen (7.98), (7.100) en (7.101) worden nu lineair zoals hieronder aangegeven

Laplace Transformation Eqs (7.102) en (7.103),
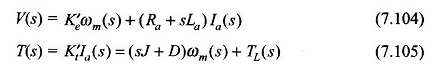
Deze vergelijkingen kunnen worden gereorganiseerd als 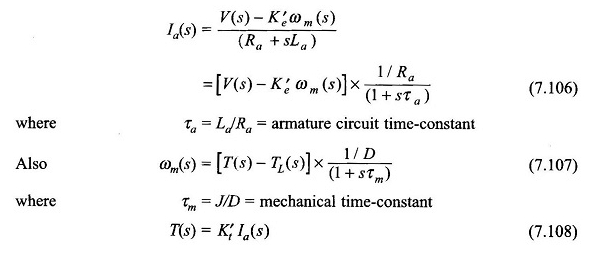
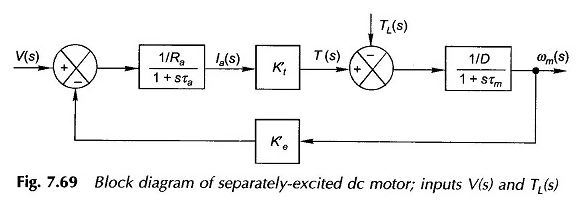
Uit vergelijkingen (7.106) – (7.108) kan het motorblokdiagram worden getekend zoals in figuur 7.69. Het is een tweede -rate feedbacksysteem met een oscillerende reactie in het algemeen. Het wordt gereduceerd tot een eenvoudig eerste -ratesysteem, als de en daarom τa wordt verwaarloosd.
Shuntgeneratorspanning Accumulatie:
De kwalitatieve verklaring van het spanningsaccumulatieproces in een shuntgenerator is al besproken. Hier zal de wiskundige behandeling van dit probleem worden gegeven, die in feite neerkomt op de oplossing van een niet -lineaire differentiaalvergelijking.
Verwijzend naar Fig. 7.70 zien we dat voor elke veldstroom de interceptie AB tussen de OCC en de RF -lijn de spanningsdaling geeft veroorzaakt door de veranderingssnelheid van φf en de onderschepping BC de daling van de weerstand tegen het veld geeft. De twee evenwicht de EMF genereerden EA (verwaarlozen ifra, de daling van de versterking) samen. Dus 
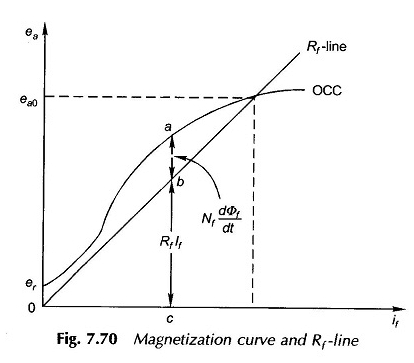
De φf-veldstroom is hoger dan de directe asluchtklofstroom φd als gevolg van het lek.
Rekening houden

Hier staat σ bekend als de dispersiecoëfficiënt.
Herinnering van Vgl. (7.3),


Het vervangen van de vergelijkingen (7.110) en (7.111) in de vergelijking. (7.109),

Vermenigvuldig de teller en de noemer met NFPAG
Of
PAG is de doordringen van lucht / na de wandeling 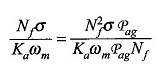
Het wordt gemakkelijk erkend dat de teller de onverzadigde waarde van de veldinductantie, LF, LF is, en de noemer is de helling van de lucht-gaplijn. Beide zijn constanten. Dus, 
Deze integrale kan grafisch worden geëvalueerd door de gebieden op een 1 / (ea – rf if) route tegen EA samen te vatten. Deze aanpak wordt gebruikt om EA tegen de tijd te plotten.
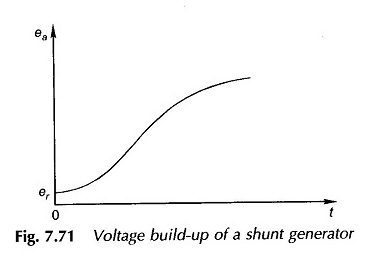
De theoretische tijd die nodig is voor de gegenereerde EMF om de vacuümwaarde te bereiken, EA0 zou oneindig zijn; Daarom wordt in de praktijk de tijd die nodig is om 0,95 EA0 te bereiken, genomen als de tijd die nodig is om EA0 te bereiken. De variatie van de EA wordt in de loop van de tijd getekend in figuur 7.71.
Het antwoord is vrij traag omdat alleen kleine spanningsverschillen (= ea – rfif) bijdragen aan de accumulatie van stromen (φf).