Transitional CC Engine Analysis:
Beginnen, remmen, snelheidsverandering en belastingverandering zijn de tijdelijke analyse van de continue huidige engine die vaak voorkomt in een industriële speler.
Men is geïnteresseerd om te weten hoe de huidige, koppel en snelheid van de rijmotor in de tijd veranderen in deze overgangsactiviteiten.
Men is ook geïnteresseerd in het kennen van energieverliezen, met name degenen die verantwoordelijk zijn voor de motorverwarming en de tijd die nodig is voor de voltooiing van de tijdelijke analyse van de DC -motor.
Deze informatie is noodzakelijk door de ontwerper om een geschikte notatie van de motor, de aard en het type van de besturingsapparatuur en de operationele kalender en de soorten beschermingsapparatuur en hun parameters te selecteren.
De dynamische equivalente circuits van CC -motoren worden weergegeven in figuur 5.12. Bronspanning v Stroom van de IA en intrek EMF -motorversterking worden aangeduid met letters onderaan de case om te benadrukken dat dit onmiddellijke waarden van variabele tijdstoren zijn.
B en J zijn respectievelijk de coëfficiënt van viskeuze wrijving in NM / RAD / SEC en het polaire traagheidsmoment in KG-M2 van het motorsysteem van de motor die bij de motoras wordt genoemd.

De spanningsvergelijking van het overgangsversterkingscircuit wordt gegeven door

Dynamiek van het motorlaadsysteem

Verder
![]()
De bovenstaande overgangsanalyse van de DC -motor is geldig voor elke DC -motor. In het geval van een opgewonden motor afzonderlijk wanneer de veldstroom constant wordt gehouden, blijft de stroom constant en zijn (5.16) en (5.17) lineaire differentiaalvergelijkingen.
In het geval van een serie -motor, vanwege de verzadiging van het magnetische circuit, is de stroom een niet -lineaire functie van de versterkingsstroom en zijn bijgevolg (5.16) en (5.17) niet -lineaire differentiaalvergelijkingen.
Zelfs als het magnetische circuit vermoedelijk lineair is door verzadiging te verwaarlozen (5.16) en (5.17) niet -lineaire differentiaalvergelijkingen zijn omdat E evenredig is met het product van IA en ωm, en T evenredig is met I2A.
Voor een serie in serie kunnen deze vergelijkingen dus niet digitaal worden opgelost door de 4e Order RunGekutta -methode of de Predictor -correctiemethode te gebruiken.
Overgangsanalyse van de geëxciteerde motor afzonderlijk met ongewone controle:
Wanneer de veldstroom constant wordt gehouden, blijft de stroom constant. Keφ vervanging door een constante K in de vergelijkingen. (5.16) tot (5.18), geeft

De vergelijking onderscheiden. (5.20) geeft
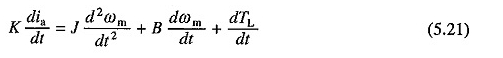
Vervangen in de vergelijking. (5.19) voor dia / dt van (5.21) en herschikking geeft de termen
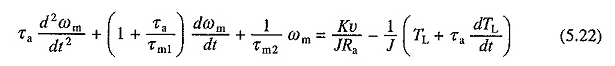
De vergelijking onderscheiden. (5.19) geeft

Vervangen in de vergelijking. (5.20) voor dωm / dt van de vergelijking. (5.23) en reorganiseer de voorwaarden
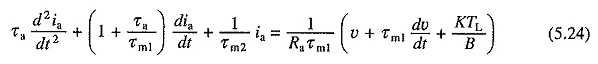
Of


De vergelijkingen (5.22) en (5.24) zijn tweede -schat lineaire differentiaalvergelijkingen en kunnen worden opgelost als de juiste beginvoorwaarden bekend zijn. Zodra de IA versus T -relatie is verkregen uit de vergelijking. (5.24), de relatie T versus t kan worden berekend.
Overgangsanalyse van het begin van de opgewonden motor afzonderlijk met de besturing van de versterking:
Een overgangsanalyse van het opstartproces zal hier worden overwogen om aan te tonen hoe de bovengenoemde vergelijkingen worden gebruikt.
Er zal worden aangenomen dat de motor wordt gestart met een constante spanning V onder de indruk van zijn terminals tegen een constant ladingskoppel TL en met een vaste weerstand RA in zijn versterkingscircuit.
Het is gebruikelijk om aan te nemen dat de motor pas begint nadat het ontwikkelde koppel het laadkoppel overschrijdt. Omdat deze motorstroom de waarde moet bereiken die het heeft gegeven door

Wanneer de motor is aangesloten op de voeding, is de beginwaarde van de stroom nul en vanwege de inductantie van het ongebruikelijke circuit, duurt het een bepaalde tijd om de waarde ervan te bereiken.
Gedurende deze hele periode, die zal worden gekwalificeerd als het eerste interval van de overgangsrespons, blijft de motor bij een stop en blijft de achterste EMF nul. De motor gedraagt zich als een eenvoudige ra – de belasting. Daarom wordt zijn stroom gegeven door

Het tweede voorbijgaande responsinterval begint nadat de stroom de waarde bereikt. Omdat V en TL constanten zijn, zijn DV / DT en DTL / DT nul. Het vervangen van deze waarden in vergelijkingen. (5.22) en (5.24) geeft
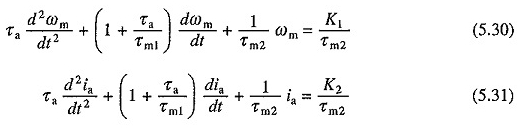
Of
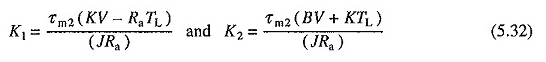
K1 en K2 vertegenwoordigen de permanente waarden van snelheid en stroomstroom met een ladingskoppel gelijk aan TL.
Initiële voorwaarden die nodig zijn voor de oplossing van vergelijkingen. (5.30) en (5.31) zijn
![]()
Aangezien aan het begin van dit interval het motorkoppel gelijk is aan het laadkoppel, van de vergelijking. (5.17)

Verder van de vergelijking. (5.16)

Gelijke oplossingen. (5.30) en (5.31) met de beginvoorwaarden gegeven door (5.33) tot (5.35), hebben de vorm:

waarbij α1 en α2 karakteristieke vergelijkingswortels zijn en worden gegeven door
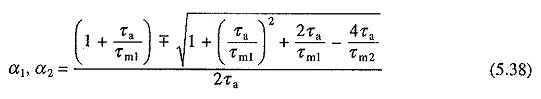
Merk op dat de bovenstaande vergelijkingen werden afgeleid door het meten van de tijd aan het begin van het tweede interval.
Voor motoren van minder dan 1000 kW zijn de wortels α1 en α2 over het algemeen reëel.
Voor grotere en middelgrote motoren, met een externe inductie verbonden in het versterkingscircuit, zoals in het geval van een helikopter en een overgangsanalyse geleverd door een DC -motor, kunnen de wortels complex zijn.
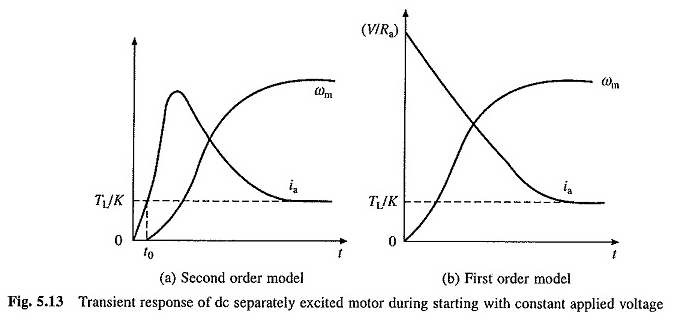
De aard van de ωm versus T- en IA versus T -curven voor start -up transiënten, wanneer de wortels echt zijn, worden weergegeven in figuur 5.13 (a).
In kleine motoren is τa erg klein vanwege een grote weerstand tegen het wikkelen van de versterking. Het kan daarom over het hoofd worden gezien. Het vervangen van τa = 0 in de vergelijkingen. (5.30) en (5.31) geeft
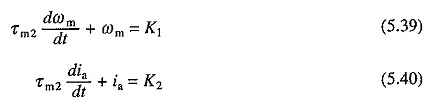
Van τa = 0 gaat de stroom naar de V / RA -waarde in nultijd. De beginvoorwaarden zijn dus
![]()
Gelijke oplossingen. (5.39) en (5.40) opbrengst

De aard van ωm ten opzichte van de krommen T en AI in vergelijking met deze vergelijkingen wordt weergegeven in figuur 5.13 (6).
Overgangsanalyse van dynamisch remmen van de opgewonden motor afzonderlijk:
Er wordt aangenomen dat een constante TL -actieve belasting op de motoras werkt. Overgangssnelheid en stroomvergelijkingen kunnen worden verkregen door een nieuwe waarde te vervangen voor de weerstand van het ongebruikelijke circuit en v = 0 in de vergelijkingen. (5.30) en (5.31). Het geeft

Ook hier vertegenwoordigen K3 en K4 respectievelijk snelheid en stroomwaarden in de evenwichtstoestand. Deze permanente werking zal plaatsvinden wanneer het actieve TL -laadkoppel is gemachtigd om de motor in de tegenovergestelde richting te drijven. De beginvoorwaarden die nodig zijn voor de oplossing van deze vergelijkingen worden als volgt verkregen:
Er wordt aangenomen dat de motor bij het initiëren van remmen in de evenwichtstoestand werkte met een TL -belastingskoppel. Dan van de vergelijking. (5.30)
![]()
Voor een algemeen geval moet K1 worden beschouwd als de initiële snelheid.
Remmen kan worden toegepast met of zonder het versterkingscircuit te openen. Wanneer het niet open is, wanneer de auto wordt overgegaan naar het remmen, wordt de continuïteit van de versterkingsstroom gehandhaafd, dan de initiële waarde van de stroom, van de vergelijking. (5.31), zal K2 zijn.
Als het echter open is, is de beginwaarde van de stroom nul. Hier gaan we ervan uit dat het open is tijdens de overgang. DUS
![]()
Nu van Eqs. (5.19) en (5.20), door v = 0, ia = 0 en ωm = k1 te vervangen.
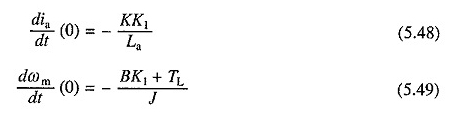
Gelijke oplossingen. (5.43) en (5.44) met de beginvoorwaarden van (5.46) tot (5.49) hebben het formulier:
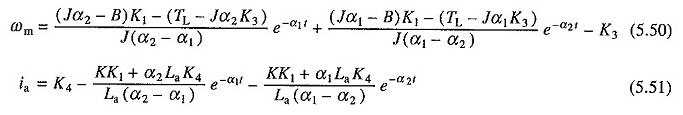
waar α1 en α2 worden gegeven door de vergelijking. (5.38).
De aard van de voorbijgaande respons onder dynamisch remmen voor het geval van reële α1 en α2 wordt geïllustreerd in figuur 5.14.
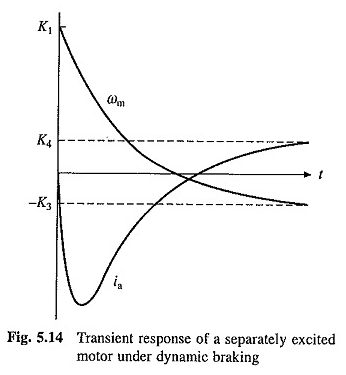
De overgangsvergelijkingen van de plug -in -inwerking worden verkregen van (5.19), (5.20), (5.22) en (5.24) vervanging – V voor v.
Energieverliezen tijdens overgangsoperaties:
Energieverliezen in de motor en in de weerstanden in het motorversterkingscircuit, als er tijdens de tijdelijke bedrijfsperiode nodig zijn om geschikte noten van de motor en weerstand te selecteren. Ze zijn ook nodig om de efficiëntie en efficiëntie van het overgangsproces te berekenen.
Vermenigvuldig beide zijden van de vergelijking. (5.16) door Ia geeft

Omdat het viskeuze wrijvingskoppel deel uitmaakt van het TL -laadkoppel, hebben we vergelijking. (5.17)

Vergelijkingen vervangen. (5.18) en (5.53) in (5.52) en integratie van de twee zijden van de resulterende vergelijking tegen tijdopbrengst
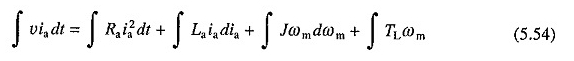
Deze vergelijking bepaalt dat op de totale energie die door de bron tijdens een overgangsproces wordt verstrekt, een onderdeel wordt verspild in de weerstand van het wapeningscircuit, het tweede gedeelte wordt opgeslagen in de inductantie van het versterkingscircuit, wordt het derde gedeelte opgeslagen in de traagheid van de mechanische delen en de rest wordt verbruikt door de belasting.
De energie die is opgeslagen in de inductie van het versterkingscircuit is over het algemeen laag in vergelijking met andere energietermen en zal daarom worden verwaarloosd in de latere analyse.
Het starten van de motor met een constante V -spanning V- en TL -oplaadkoppel worden nu overwogen.
Van

waar ωm0 de ideale snelheid is zonder belasting. Vergelijkingen. (5.54) en (5.55)

De vergelijking (5.56) geeft een uitdrukking voor het verlies van energie in de weerstand van het versterkingscircuit van de machine. Wanneer begonnen zonder belasting, zal de uiteindelijke snelheid (evenwichtstoestand) ωm0 zijn. Daarom is het verlies van energie in elke E0 -belastingsconditie

Het is interessant om op te merken dat het verlies van energie in het motorversterkingscircuit tijdens de start -up zonder belasting gelijk is aan de kinetische energie die is opgeslagen in de roterende delen van de motor met een stabiele toestandsnelheid.
Bovendien is het onafhankelijk van de duur van het uitgangsproces, de aard van de kuikensnelheid en de kenmerken van de motorsnelheidstroom, het aantal stadia van opstartweerstand en de waarde van de reister in elke stap.
Aangezien ωm0 niet erg verschillen van de snelheid in de evenwichtstoestand met de TL -belasting op de motoras, de eerste term op RHS van de vergelijking. (5.56) Vertegenwoordigt ongeveer het verlies van koper tijdens het starten onder een lading en wat er is gezegd over E0 is ook van toepassing op deze termijn.
De tweede term hangt af van de kenmerken van de motorsnelheidsbelasting en de waarde van de startweerstand. Deze term wordt weergegeven door het gearceerde gebied van figuur 5.15.

Zoals hierboven aangegeven, blijft de eerste term aan de rechterkant van (5.56) ongewijzigd met de verandering in startweerstand. Het kan echter worden verlaagd door een verminderde start -UP -spanningsmethode. Overweeg de zaak waarin de bronspanning wordt toegepast in een aantal gelijke stappen. Het eerste deel van het MTH Koperverlies zal zijn
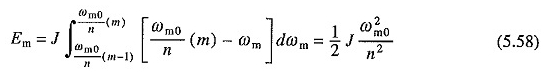
Aangezien dit deel van het verlies van koper op alle n stappen hetzelfde zal zijn, wordt totaal geen verlies van koper tijdens de start

Vergelijking hiervan met de vergelijking. (5.57) toont aan dat verlies van koper zonder belasting is verminderd met een factor n.
Laten we het verlies vervolgens onderzoeken tijdens het reostatische remmen. Door V = 0 te vervangen, door het te verwaarlozen en aan te nemen dat het belastingskoppel constant en gelijk is aan TL, kan de volgende vergelijking worden afgeleid van (5.52) en (5.53)
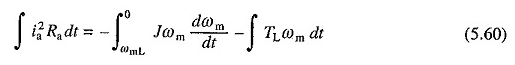
Er is aangenomen dat vóór het remmen de motor in de evenwichtstoestand werkte tegen een passief laadkoppel TL met een ωML -snelheid. Over EQ -integratie. (5.60) weergegeven

Deze vergelijking geeft aan dat de belasting een deel van de opgeslagen kinetische energie absorbeert en dat de rest is verdwenen in de vorm van een verlies van koper.
Voor verstopping, over de vervanging van —V voor V en de = 0, in de vergelijkingen. (5.52) en (5.53) De volgende vergelijking wordt verkregen voor het verlies van koper
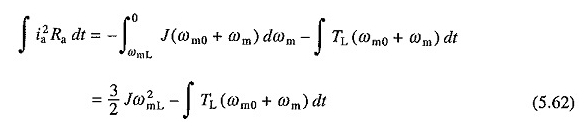
Vergelijkingen. (5.61) en (5.62) Koperen verliezen zonder belasting onder remmen en dynamische stekker zijn respectievelijk 1/2 Jω20 en 3/2 Jω20. Het verlies tijdens de verbinding zal dus drie keer dit zijn tijdens dynamisch remmen.
Gezien het feit dat tijdens de plug -in -in -in -in -in -in -kinetische energie van de roterende stukken slechts 1/2 Jω2M0 is, wordt de rest Jω2M0 uit de voeding gehaald.
Overgangsanalyse van de geëxciteerde motor afzonderlijk met veldregeling:
Ofwel de constante versterkingspanning. NU
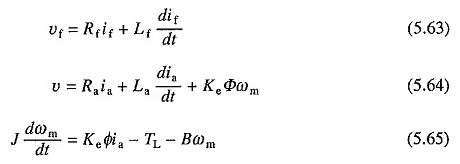
Hier is φ een niet -lineaire functie van IF. Als de verzadiging wordt verwaarloosd en φ verondersteld wordt evenredig te zijn met SO (5.64) en (5.65) kunnen worden geschreven als

waar k ′ = KEKφ.
Vanwege de termen K′ifΩm en k′ifia, waarbij het product van twee variabelen (5.66) en (5.67) niet zijn, zijn niet -lineaire vergelijkingen, zelfs als verzadiging is verwaarloosd.
Deze analyse kan dus worden uitgevoerd met behulp van digitale methoden voor het oplossen van niet-lineaire differentiaalvergelijkingen zoals 4e Runege-Kutta en voorspellende methoden voor de hoek.
Een speciaal geval met landcontrole treedt op wanneer de versterkingsstroom constant wordt gehandhaafd. Vervolgens wordt de dynamiek van het motorlaadsysteem beschreven door de vergelijking. (5.63) met de volgende vergelijking:

waar ka = kekφia en ia de stroom van versterking is.
Van de vergelijking. (5.68) Expressie van if en dif / dt kan worden verkregen. Vervang ze in de vergelijking. (5.63) en reorganiseer de “voorwaarden geeft

Of

De motor kan worden geanalyseerd op zijn overgangsrespons met behulp van de vergelijking. (5.69) op voorwaarde dat de beginvoorwaarden bekend zijn. De initiële waarde van ωm zal van het werkpunt naar de evenwichtstoestand worden bekend, onmiddellijk vóór de transiënten en de beginwaarde van dωm / dt wordt berekend uit de vergelijking. (5.68).

