Silnik DC z momentem obrotowym prędkości:
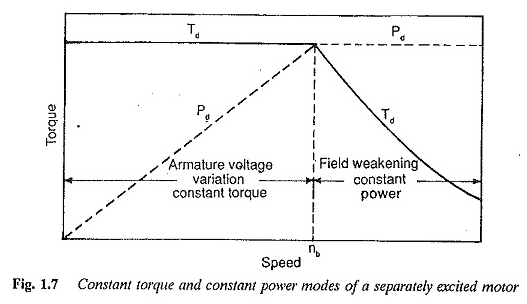
Poprzednia dyskusja pokazuje, że zmienność napięcia zbrojenia zapewnia prędkości pełzania. Prosta metoda reostatyczna zapewnia silnik bocznika DC charakterystyczny dla momentu obrotowego prędkości przy niewielkiej twardości i niewielkiej stabilności.
Z drugiej strony kontrola Ward Leonarda (płynna odmiana napięcia) daje płaską cechę z rozsądną twardością i stabilnością, ale wysoki koszt początkowy. Prosta metoda o niskim koszcie początkowym, aby uzyskać prędkości pełzania z wystarczającą twardością, przedstawiono na rysunku 1.8.
Konwencjonalna kontrola reostatyczna z opornością szeregową z wzmocnieniem jest modyfikowana przez strzelanie do wzmocnienia z niską opornością. Zmieniając wartości serii i rezystorów bocznikowych, cechy Chilled prędkości można zaprojektować tak, aby miały pożądany kształt.
W prostej kontroli reostatycznej przy użyciu jedynie oporności szeregowej napięcie przez schronienie wynosi V. Prędkość próżniową decyduje V, bez względu na wartość Rs. Jeśli zbrojenie jest przeciwieńowane przez RSH, napięcie przez ramkę staje się niższe niż V, nawet bez obciążenia.
Pusta prędkość spada do żądanej wartości z odpowiednimi wartościami RS i RSH. Im mniejsza wartość RSH, tym bardziej napięcie to napięcie przez ramkę bez obciążenia. Wreszcie prędkość nie obciążenia zmniejsza się. Wartość RSH jest również skuteczna w charakterystyce dania.

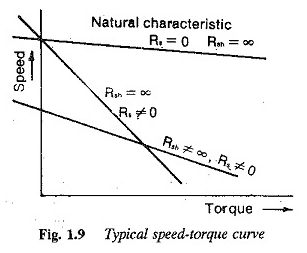
Typowe cechy prędkości pisklęcia są reprezentowane na rycinie 1.9, na której naturalna charakterystyka silnika DC Shunt i cecha z prostą kontrolą reostatyczną. Tę modyfikację można zastosować, jeśli wymagana jest stabilna operacja o niskiej prędkości. Można go używać do dokładnego zatrzymania czytelnika. Modyfikując wartość RSH, prędkość można zmniejszyć do bardzo niskiej wartości, a odpowiednie hamowanie mechaniczne można zastosować, aby mieć określony zatrzymanie. 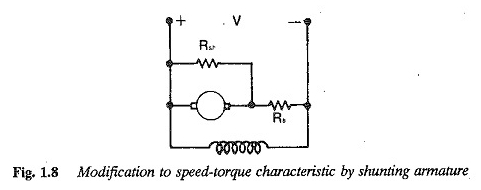
Odnosząc się do rysunku 1.8, mamy 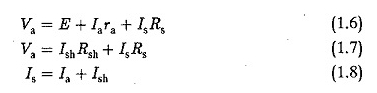
Korzystając z tych równań, mamy

Również z równań (1.8) i (1.7)

Wykorzystanie tych relacji w równaniu. (1.6) Mamy
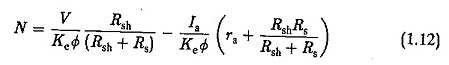
Zastąpić / a Pod względem TD mamy
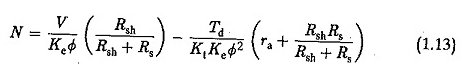
Charakterystyka szybkiego podsumowania jest reprezentowana na rysunku 1.9. Poniższe punkty wynikają z rysunku:
1. Prędkość obciążenia (TD = 0) maleje do 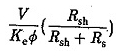
jako wartość 
Wartość RSH jest niższa, wartość ta jest mniejsza. Nachylenie zmniejsza się również, jeśli RSH jest mały. W ten sposób twardość jest ulepszona, a stabilne działanie jest zapewniane w odniesieniu do prostej kontroli reostatycznej.
2. Gładka kontrola prędkości zależy od tego, jak RSH i RS są zróżnicowane. Kontrola prędkości jest zdumiona, ponieważ rezystory mogą się różnić w rozłożonym żeglarze.
3. Cavage poniżej podstawowej prędkości jest możliwa. Sama pusta prędkość zmienia się po zmianach RSH. Wyraźny spadek pustej prędkości można zaobserwować, gdy RSH zostanie zmniejszony. Kontrola prędkości uzyskuje się poprzez zmianę wartości Rs.
Metoda jest równoważna z wzmocnieniem pola i daje wyniki podobne do tych uzyskanych przez zwiększenie prądu pola do danego prądu zbrojenia.
4. Metoda nadaje się do stałego obciążeń momentu obrotowego, tak aby prąd zbrojenia ma wartość nominalną.
5. Metoda jest odpowiednia, jeśli jest dokładny przystanek
6. Nie jest to ekonomiczne dla ciągłego działania. Straty RSH i RS sprawiają, że system jest nieskuteczny. Metodę można zastosować, jeśli stabilne prędkości rampy są niezbędne przez krótkie okresy.
