Przejściowa analiza silnika CC:
Rozpoczęcie, hamowanie, zmiana prędkości i zmiana obciążenia to przejściowa analiza ciągłego silnika prądu, która występuje zwykle u gracza przemysłowego.
Zainteresowany jest wiedza o tym, jak zmieniają się prąd, moment obrotowy i prędkość silnika napędowego w czasie w tych operacjach przejściowych.
Jest również zainteresowany znajomością strat energii, w szczególności tych odpowiedzialnych za ogrzewanie silnika i czas potrzebny na zakończenie przejściowej analizy silnika DC.
Informacje te są niezbędne przez projektanta, aby wybrać odpowiednią notację silnika, charakter i rodzaj jego sprzętu sterującego oraz kalendarza operacyjnego oraz rodzajów urządzeń ochronnych i ich parametrów.
Dynamiczne równoważne obwody silników CC przedstawiono na rysunku 5.12. Napięcie źródłowe v prąd IA i cofanie silnika EMF są oznaczone literami na dole obudowy, aby podkreślić, że są to natychmiastowe wartości zmiennych ilości czasu.
B i J są odpowiednio współczynnikiem tarcia lepkiego w NM / RAD / SEC oraz polarnym momentem bezwładności w kg-m2 układu silnikowego silnika wymienionego w wałku silnika.

Równanie napięcia przejściowego obwodu zbrojeniowego jest podane przez

Dynamika systemu obciążenia silnika

Dalej
![]()
Powyższa analiza przejściowa silnika DC jest ważna dla każdego silnika DC. W przypadku podekscytowanego silnika osobno, gdy prąd pola jest utrzymywany stałą, przepływ pozostaje stały i (5.16) i (5.17) są liniowymi równaniami różniczkowymi.
W przypadku silnika szeregowego, ze względu na nasycenie obwodu magnetycznego, przepływ jest nieliniową funkcją prądu zbrojeniowego, a zatem (5.16) i (5.17) są nieliniowe równania różniczkowe.
Nawet jeśli obwód magnetyczny jest podobno liniowy poprzez zaniedbanie nasycenia, (5.16) i (5.17) są nieliniowymi równaniami różnicowymi, ponieważ E jest proporcjonalne do iloczyn IA i ωM, a T jest proporcjonalne do I2a.
Zatem dla serii szeregowej, równań tych nie można rozwiązać cyfrowo za pomocą czwartej metody Rungekutta lub metody korektora predykcyjnego.
Przejściowa analiza silnika wzbudzonego osobno z niezwykłą kontrolą:
Gdy prąd pola jest utrzymywany na stałym poziomie, przepływ pozostaje stały. Keφ zastąpienie stałym k w równaniach. (5.16) do (5.18), daje

Różnicowanie równania. (5.20) daje
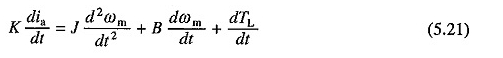
Zastępowanie w równaniu. (5.19) dla dia / dt (5.21) i rearanżacji podania warunków
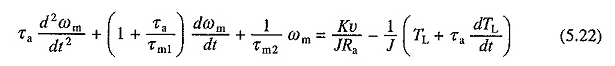
Różnicowanie równania. (5.19) daje

Zastępowanie w równaniu. (5.20) dla DωM / dt równania. (5.23) i zreorganizować warunki
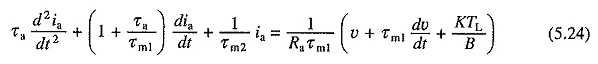
Lub


Równania (5.22) i (5.24) są drugim liniowym równaniami różniczkowymi i można je rozwiązać, jeśli znane są odpowiednie warunki początkowe. Po uzyskaniu związku IA vs T z równania. (5.24), można obliczyć związek T vs T.
Przejściowa analiza początkowego silnika wzbudzonego osobno przy kontroli wzmocnienia:
Rozważa się tutaj przejściową analizę procesu uruchamiania w celu wykazania, w jaki sposób stosowane są wyżej wymienione równania.
Zakłada się, że silnik uruchamia się ze stałym napięciem V wrażenie na jego zaciskach przed TL stałego ładunku i ze stałym rezystancją RA w obwodzie wzmacniającym.
Zwykle można założyć, że silnik zaczyna się dopiero po tym, jak jego rozwinięty moment obrotowy przekracza moment obrotowy. Ponieważ ten prąd silnika powinien osiągnąć wartość podaną przez

Gdy silnik jest podłączony do zasilania, początkowa wartość prądu wynosi zero i ze względu na indukcyjność nietypowego obwodu zajmuje określony czas, aby osiągnąć wartość.
W całym tym okresie, który zostanie zakwalifikowany jako pierwszy interwał reakcji przejściowej, silnik pozostaje na zatrzymaniu, a zatem jego tylny EMF pozostaje zerowy. Silnik zachowuje się jak prosty RA – obciążenie. Dlatego jego prąd jest podany przez

Drugi przedział odpowiedzi przejściowej rozpoczyna się po osiągnięciu prądu. Ponieważ V i TL są stałymi, DV / DT i DTL / DT będą wynosić zero. Podstawiając te wartości w równaniach. (5.22) i (5.24) daje
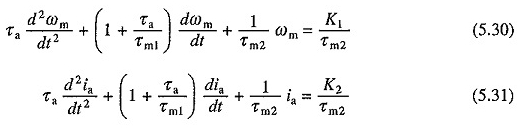
Lub
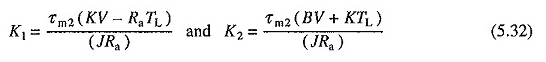
K1 i K2 reprezentują stałe wartości prędkości i prądu prądu z momentem obrotowym ładowania równym TL.
Wstępne warunki niezbędne do rozwiązania równań. (5.30) i (5.31) są
![]()
Biorąc pod uwagę, że na początku tego przedziału moment obrotowy silnika jest równy momentowi obciążenia z równania. (5.17)

Dalej od równania. (5.16)

Równe rozwiązania. (5.30) i (5.31) z warunkami początkowymi podanymi przez (5.33) do (5.35), będą miały formularz:

gdzie α1 i α2 są charakterystycznymi korzeniami równań i są podawane przez
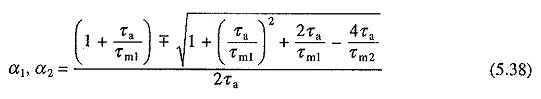
Należy zauważyć, że powyższe równania uzyskano przez pomiar czasu na początku drugiego przedziału.
W przypadku silników mniejszych niż 1000 kW korzenie α1 i α2 są ogólnie prawdziwe.
W przypadku silników o większych i średnich, z zewnętrzną indukcyjnością połączoną w obwodzie zbrojenia, jak w przypadku helikoptera i analizy przejściowej dostarczonej przez silnik prądu stałego, korzenie mogą być złożone.
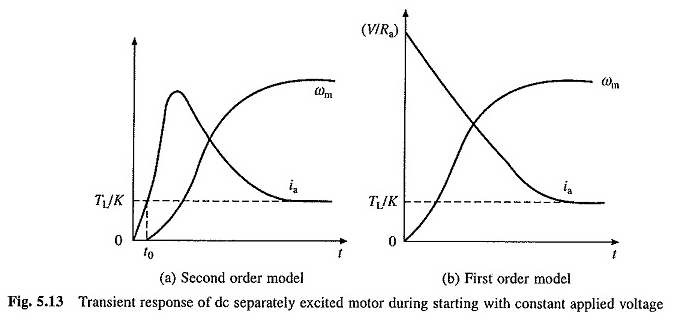
Charakter krzywych ωm vs t i Ia vs t dla start -up, gdy korzenie są rzeczywiste, przedstawiono na rysunku 5.13 (a).
W małych silnikach τa jest bardzo mały ze względu na wielką odporność na uzwojenie wzmocnienia. Można go zatem przeoczyć. Podstawianie τa = 0 w równaniach. (5.30) i (5.31) daje
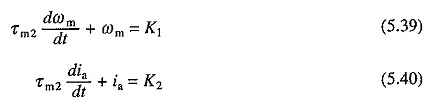
Od τa = 0 prąd przechodzi do wartości v / ra w czasie zerowym. Zatem warunki początkowe są
![]()
Równe rozwiązania. (5.39) i (5.40) wydajność

Charakter ωM w odniesieniu do krzywych T i Ai w porównaniu z tymi równaniami przedstawiono na rysunku 5.13 (6).
Przejściowa analiza dynamicznego hamowania podekscytowanego silnika osobno:
Zakłada się, że na wale silnikowym działa stałe obciążenie aktywne TL. Prędkość przejściową i równania prądowe można uzyskać, zastępując nową wartość rezystancją nietypowego obwodu i v = 0 w równaniach. (5.30) i (5.31). Daje

Również tutaj – K3 i K4 reprezentują odpowiednio prędkość i wartości prądowe w stanie równowagi. Ta stała operacja nastąpi, gdy aktywny moment obciążenia TL jest upoważniony do napędzania silnika w przeciwnym kierunku. Początkowe warunki niezbędne do rozwiązania tych równań są uzyskiwane w następujący sposób:
Zakłada się, że podczas inicjacji hamowania silnik działał w stanie równowagi z momentem obciążenia TL. Następnie z równania. (5.30)
![]()
W przypadku ogólnego przypadku K1 należy uznać za prędkość początkową.
Hamowanie można zastosować z otwieraniem obwodu zbrojeniowego lub bez niego. Gdy nie jest otwarte, gdy samochód jest przechodzący na hamowanie, będzie utrzymywana ciągłość prądu zbrojenia, a następnie wartość początkowa prądu, z równania. (5.31), będzie K2.
Jeśli jednak jest otwarta, początkowa wartość prądu wyniesie zero. Tutaj zakładamy, że jest otwarty podczas przejścia. WIĘC
![]()
Teraz z równania. (5.19) i (5.20), zastępując v = 0, Ia = 0 i ωm = k1.
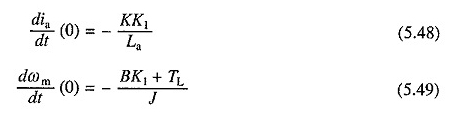
Równe rozwiązania. (5.43) i (5.44) z początkowymi warunkami od (5.46) do (5.49) będą miały formularz:
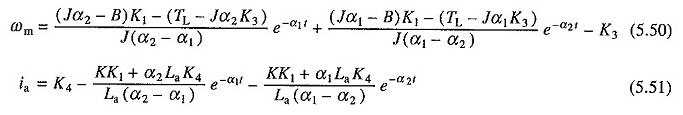
gdzie α1 i α2 są podawane przez równanie. (5.38).
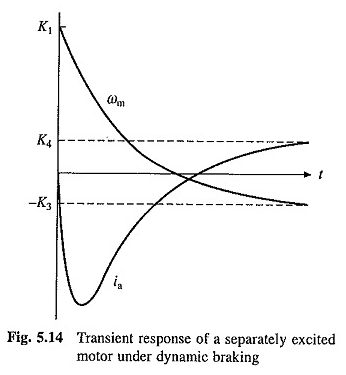
Charakter reakcji przejściowej przy dynamicznym hamowaniu w przypadku rzeczywistego α1 i α2 pokazano na rycinie 5.14.
Równania przejściowe operacji wtyczki są uzyskiwane z (5.19), (5.20), (5.22) i (5.24) podstawy – v za v.
Straty energii podczas operacji przejściowych:
Straty energii w silniku i rezystorach w obwodzie wzmacniającym silnik, jeśli w okresie przejściowym są konieczne do wyboru odpowiednich nut silnika i oporu. Są one również niezbędne do obliczenia wydajności i wydajności procesu przejściowego.
Pomnóż obie strony równania. (5.16) przez IA daje

Ponieważ lepki moment obrotowy tarcia jest częścią momentu obciążenia TL, mamy równanie. (5.17)

Zastępowanie równań. (5.18) i (5.53) w (5.52) i integracja dwóch stron powstałego równania z wydajnością czasu
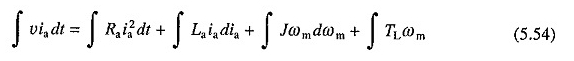
Równanie to stanowi, że na całkowitej energii dostarczonej przez źródło podczas procesu przejściowego część jest marnowana w rezystancji obwodu zbrojenia, druga część jest przechowywana w indukcyjności obwodu zbrojenia, trzecia część jest przechowywana w bezwładności części mechanicznych, a reszta jest spożywana przez ładunek.
Energia przechowywana w indukcyjności obwodu zbrojenia jest ogólnie niski w porównaniu z innymi terminami energii i dlatego będzie zaniedbywana w późniejszej analizie.
Uruchamianie silnika o stałym napięcie V i momencie obrotowym TL jest teraz brane pod uwagę.
Z

gdzie ωm0 jest idealną prędkością bez obciążenia. Równania. (5.54) i (5.55)

Równanie (5.56) daje wyrażenie utraty energii w odporności obwodu wzmacniającego maszynę. Po uruchomieniu bez obciążenia prędkość końcowa (stan równowagi) wynosi ωm0. Dlatego utrata energii w dowolnym warunkach obciążenia E0 wynosi

Warto zauważyć, że utrata energii w obwodzie wzmacniającym silnik podczas uruchomienia bez obciążenia jest równa energii kinetycznej przechowywanej w obrotowych częściach silnika o stabilnej prędkości stanu.
Ponadto jest niezależny od czasu trwania procesu początkowego, charakteru prędkości pisklęcia i charakterystyk prądu prędkości silnika, liczby etapów oporu start-upu i wartości powtórzenia na każdym etapie.
Ponieważ ωM0 nie będzie się bardzo różnić od prędkości w stanie równowagi z obciążeniem TL na wałku silnika, pierwszy okres na RHS równania. (5.56) w przybliżeniu reprezentuje utratę miedzi podczas uruchamiania pod dowolnym obciążeniem, a to, co zostało powiedziane o E0, dotyczy również tego terminu.
Drugi termin zależy od charakterystyki obciążenia prędkości silnika i wartości oporu początkowego. Termin ten jest reprezentowany przez zacieniony obszar z rysunku 5.15.

Jak wskazano powyżej, pierwszy termin po prawej stronie (5.56) pozostaje niezmieniony ze zmianą oporu początkowego. Można go jednak obniżyć metodą zmniejszonego napięcia startowego. Rozważ przypadek, w którym napięcie źródłowe jest stosowane w wielu równych krokach. Pierwsza część MTH Miedź będzie
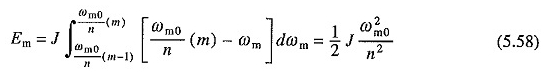
Ponieważ ta część utraty miedzi będzie taka sama na wszystkich n etapach, całkowita utrata miedzi podczas startu staje się

Porównanie tego z równaniem. (5.57) pokazuje, że utrata miedzi bez obciążenia została zmniejszona o współczynnik n.
Następnie zbadajmy utratę podczas hamowania reostatycznego. Podstawiając v = 0, zaniedbując go i zakładając, że moment obciążenia jest stały i równy TL, następujące równanie można wyprowadzić z (5.52) i (5.53)
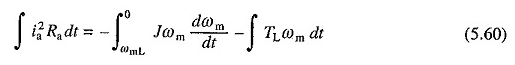
Założono, że przed hamowaniem silnik działał w stanie równowagi w stosunku do pasywnego momentu ładunku TL z prędkością ωml. W zakresie integracji EQ. (5.60) renderowany

Równanie to wskazuje, że obciążenie pochłania część przechowywanej energii kinetycznej i że reszta jest rozpraszana w postaci utraty miedzi.
Do zatykania, na podstawieniu —V dla V i = 0, w równaniach. (5.52) i (5.53) uzyskano następujące równanie dla utraty miedzi
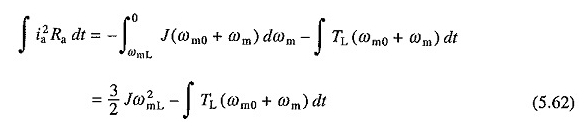
Równania. (5.61) i (5.62) Straty miedzi bez obciążenia pod hamowaniem i wtyczką dynamiczną wyniesie odpowiednio 1/2 Jω20 i 3/2 Jω20. Zatem utrata podczas połączenia będzie trzykrotnie to podczas dynamicznego hamowania.
Biorąc pod uwagę, że podczas energii wtyczki uzyskanej z energii kinetycznej elementów obrotowych wynosi tylko 1/2 jω2m0, reszta jω2m0 jest pobierana z zasilania.
Przejściowa analiza silnika wzbudzonego osobno z kontrolą pola:
Albo ciągłe napięcie wzmacniające. TERAZ
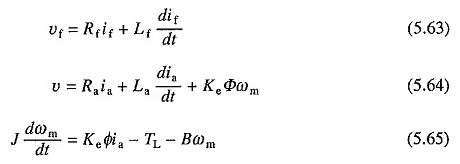
Tutaj φ jest funkcją nieliniową IF. Jeśli nasycenie jest zaniedbane, a φ ma być proporcjonalne do SO (5.64) i (5.65) można zapisać jako

gdzie k ′ = keKφ.
Ze względu na terminy K′IFωM i K’IFIA, które obejmują iloczyn dwóch zmiennych (5.66) i (5.67) są równaniami nieliniowymi, nawet jeśli nasycenie zostało zaniedbane.
W ten sposób analizę tę można przeprowadzić przy użyciu metod cyfrowych do rozwiązywania nieliniowych równań różniczkowych, takich jak czwarte metody Runege-Kutta i predykcyjnych rogów.
Specjalny przypadek z kontrolą gruntów występuje, gdy prąd wzmacniający jest utrzymywany na stałym poziomie. Następnie dynamika układu obciążenia silnika jest opisana przez równanie. (5.63) z następującym równaniem:

gdzie ka = kekφia i IA jest prądem zbrojenia.
Równania. (5.68) Można uzyskać ekspresję IF i DIF / DT. Wymień je w równaniu. (5.63) i reorganizować „Warunki

Lub

Silnik można przeanalizować pod kątem odpowiedzi przejściowej za pomocą równania. (5.69) pod warunkiem, że warunki początkowe są znane. Wartość początkowa ωM będzie znana od punktu roboczego do stanu równowagi bezpośrednio przed przejściami, a wartość początkowa DωM / dt oblicza się z równania. (5.68).

