Motor CC excitado separadamente para análise dinâmica:
Motor CC excitado separadamente para análise dinâmica – as máquinas CC são bastante versáteis e são capazes de fornecer uma variedade de características VA e na velocidade de velocidade por combinações apropriadas de vários enrolamentos de campo.
Com os controles semicondutores, suas velocidades e saídas podem ser facilmente controladas em uma ampla faixa para dieta dinâmica e permanente. Ao adicionar o circuito de feedback, as características da máquina ainda podem ser modificadas. O objetivo desta seção é estudar máquinas CC em referência às suas características dinâmicas.
Para ilustração, considere a máquina CC excitada representada separadamente esquematicamente na Figura 7.68. Para facilitar a análise, são feitas as seguintes hipóteses:
- O eixo do quadro MMF é fixado no espaço, ao longo do eixo Q.
- O efeito desmagnetizante da reação interijack é negligenciado.
- O circuito magnético deve ser linear (sem histerese e saturação). Consequentemente, todas as indutâncias (que entraram em jogo em análise dinâmica) são consideradas constantes.
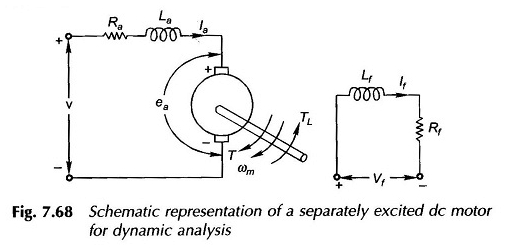
Os dois parâmetros de indutância que aparecem na Figura 7.68 são definidos abaixo:
- A = auto-indutância do reforço causada pelo fluxo de reforço; Isso é muito pequeno e pode ser negligenciado sem provocar um erro grave na análise dinâmica
- LF = auto-indução do enrolamento de campo; É grande o suficiente para o campo de derivação e deve ser levado em consideração
Indutância mútua (entre campo e reforço) = 0; Porque os dois estão na quadratura espacial.
Além disso, para o mecanismo CC excitado separadamente para uma análise dinâmica, é prático usar a velocidade RAD / S em vez de RPM.
Aplique a lei de Kirchhoff ao circuito de reforço,
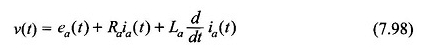
Ou
![]()
O mesmo para o circuito de campo,
![]()
Para a operação do automóvel, o mecanismo CC excitado separadamente para uma análise dinâmica para o sistema mecânico é

Ou
J = momento de inércia do motor e carga em nms2
D = coeficiente de amortecimento visque representando uma perda de torque de torque, nm rad / s
O armazenamento de energia está associado a campos magnéticos produzidos por IF e AI e à energia cinética das peças rotativas. As equações acima são um conjunto de equações de estado não lineares (devido a produtos se (t) ωm e se (t) Ia (t) com variáveis de estado se, IA e ωm. A solução deve ser obtida digitalmente.
Funções de transferência e diagrama de blocos do motor CC excitado separadamente:
No caso linear único linear da resposta do motor a alterações na tensão de embutimento, supõe -se que a tensão do campo seja constante e que o estado de equilíbrio exista no circuito de campo, ou seja, se = constante. As equações (7,98), (7.100) e (7.101) agora ficam lineares, conforme indicado abaixo

Eqs de transformação de Laplace (7.102) e (7.103),
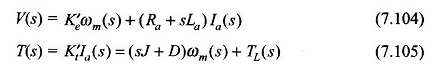
Essas equações podem ser reorganizadas como 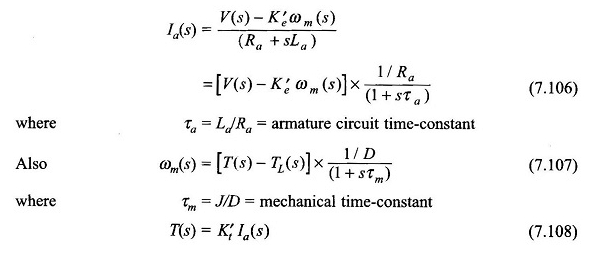
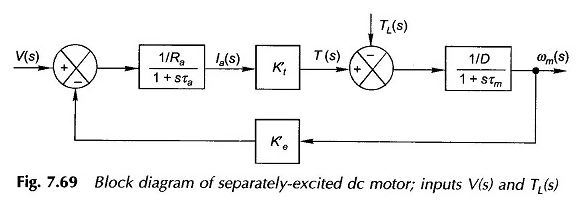
Das equações (7.106) – (7.108), o diagrama do bloco do motor pode ser desenhado como na Figura 7.69. É um sistema de feedback de segunda taxa com uma resposta oscilatória em geral. É reduzido a um sistema simples de primeira linha, se o e, portanto, τa for negligenciado.
Acumulação de tensão do gerador de derivação:
A explicação qualitativa do processo de acumulação de tensão em um gerador de derivação já foi discutida. Aqui, o tratamento matemático desse problema será dado, que de fato se resume à solução de uma equação diferencial não linear.
Referindo -se à Fig. 7.70, vemos que, para qualquer corrente de campo, a interceptação AB, entre a linha OCC e a RF, fornece a queda de tensão causada pela taxa de mudança de φf e a interceptação BC fornece a queda na resistência ao campo. Os dois equilíbrio o EMF gerou EA (negligenciando a IFRA, a queda do reforço) juntos. Então 
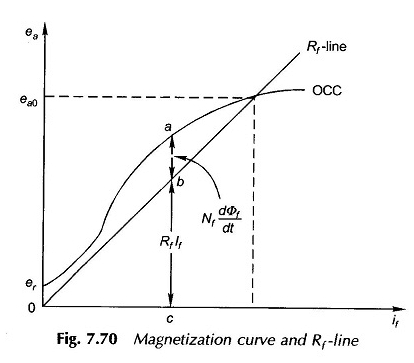
O fluxo de campo φf é maior que o fluxo de gap de ar direto do eixo φd devido ao vazamento.
Levando em consideração

Aqui, σ é conhecido como o coeficiente de dispersão.
Recordando a Eq. (7.3),


Substituindo as equações (7.110) e (7.111) na equação. (7.109),

Multiplique o numerador e o denominador por NFPAG
Ou
PAG é a permeance da caminhada aérea / pós 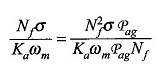
É facilmente reconhecido que o numerador é o valor insaturado da indutância de campo, LF, e o denominador é a inclinação da linha de gap-ar. Ambos são constantes. Então, 
Essa integral pode ser avaliada graficamente resumindo as áreas em uma rota 1 / (EA – RF IF) contra o EA. Essa abordagem é usada para plotar EA contra o tempo.
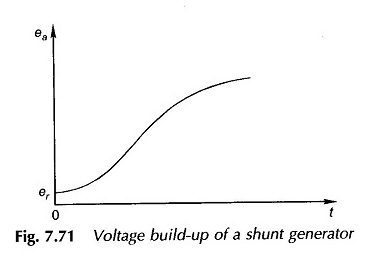
O tempo teórico necessário para a EMF gerada atingir o valor a vácuo, o EA0 seria infinito; Portanto, na prática, o tempo necessário para atingir 0,95 EA0 é tomado como tempo necessário para chegar ao EA0. A variação do EA ao longo do tempo é desenhada na Figura 7.71.
A resposta é bastante lenta porque apenas pequenas diferenças de tensão (= ea – rfif) contribuem para o acúmulo de fluxos (φf).