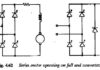
CC motoru dinamik analiz için ayrı ayrı uyarıldı:
CC motoru dinamik analiz için ayrı ayrı uyarılmıştır – CC makineleri oldukça çok yönlüdür ve çeşitli alan sargılarının uygun kombinasyonları ile çeşitli özellikler VA ve hız hızında verebilir.
Yarı iletken kontrolleri ile, hızları ve çıkışları dinamik ve kalıcı diyet için geniş bir aralıkta kolayca kontrol edilebilir. Geri bildirim devresini ekleyerek, makinenin özellikleri hala değiştirilebilir. Bu bölümün amacı DC makinelerini dinamik özelliklerine göre incelemektir.
İllüstrasyon için, Şekil 7.68’de şematik olarak ayrı ayrı temsil edilen uyarılmış CC makinesini düşünün. Analizi kolaylaştırmak için aşağıdaki hipotezler yapılır:
- MMF çerçevesinin ekseni, uzayda, Q ekseni boyunca sabitlenmiştir.
- İnterijack reaksiyonunun demagnetize edici etkisi ihmal edilir.
- Manyetik devrenin doğrusal olması gerekir (histerezis ve doygunluk yok). Sonuç olarak, tüm endüktanların (dinamik analizde devreye giren) sabit olduğu düşünülmektedir.
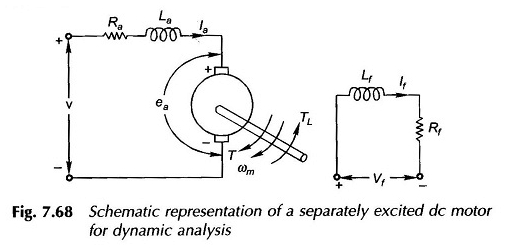
Şekil 7.68’de görünen iki endüktans parametresi aşağıda tanımlanmıştır:
- Takviye akışının neden olduğu takviyenin = kendi kendine indüksiyonu; Bu oldukça küçük ve dinamik analizde ciddi bir hata provoke etmeden ihmal edilebilir
- LF = Saha sarısının kendi kendine indüksiyonu; Şant alanı için yeterince büyüktür ve dikkate alınmalıdır
Karşılıklı endüktans (alan ve takviye arasında) = 0; Çünkü ikisi uzay dörtgeninde.
Buna ek olarak, heyecanlı CC motoru dinamik bir analiz için ayrı ayrı, RPM yerine rad / s hızını kullanmak pratiktir.
Kirchhoff Yasasını Takviye Devresine uygulayın,
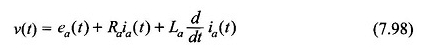
Veya
![]()
Saha devresi için de aynısı,
![]()
Otomobilin çalışması için, mekanik sistem için dinamik bir analiz için CC motoru ayrı ayrı uyarılmıştır.

Veya
J = NMS2’de Motor Ataleti ve Yük Moment
D = tork tork kaybını temsil eden visque sönümleme katsayısı, nm rad / s
Enerji depolama, IF ve AI tarafından üretilen manyetik alanlarla ve döner parçaların kinetik enerjisi ile ilişkilidir. Yukarıdaki denklemler bir dizi doğrusal olmayan durum denklemleri kümesidir (IF (t) ωm ve (t) ia (t) IF (t) ia (t) IF (t) Ia (t) IS, IA ve ωm. Çözelti dijital olarak elde edilmelidir.
Aktarım fonksiyonları ve motor bloğu diyagramı CC ayrı ayrı uyarılır:
Motor voltajındaki değişikliklere motor tepkisinin tek doğrusal doğrusal durumunda, alan voltajının sabit olduğu ve denge durumunun alan devresinde, yani = sabit olup olmadığı varsayılmaktadır. (7.98), (7.100) ve (7.101) denklemleri, aşağıda belirtildiği gibi doğrusal hale gelir

Laplace Dönüşümü EQS (7.102) ve (7.103),
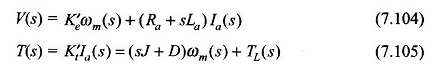
Bu denklemler olarak yeniden düzenlenebilir: 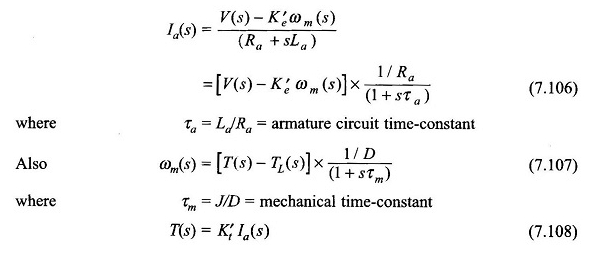
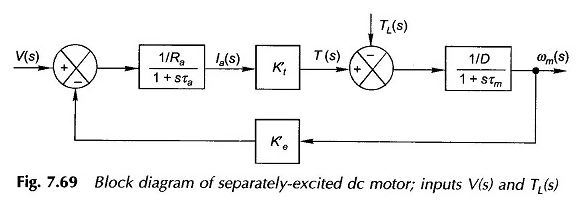
Denklemlerden (7.106) – (7.108), motor bloğu diyagramı Şekil 7.69’da olduğu gibi çizilebilir. Genel olarak salınım tepkisi olan ikinci bir geri besleme sistemidir. Eğer ve dolayısıyla τA ihmal edilirse, basit bir ilk -rate sistemine indirgenir.
Şant jeneratör gerginliği birikimi:
Bir şönt jeneratöründe gerginlik birikimi sürecinin nitel açıklaması zaten tartışılmıştır. Burada, aslında doğrusal olmayan bir diferansiyel denklemin çözümüne inen bu sorunun matematiksel tedavisi verilecektir.
Şekil 7.70’e atıfta bulunarak, herhangi bir alan akımı için, OCC ve RF çizgisi arasındaki AB müdahalesinin, φF’nin değişim hızının neden olduğu voltaj düşüşünü verdiğini ve BC’nin müdahalenin alana direnç düşüşünü verdiğini görüyoruz. İkisi EMF’nin EA (IFRA’yı ihmal ederek, takviyenin düşüşünü ihmal eder) dengesini bir araya getirir. Bu yüzden 
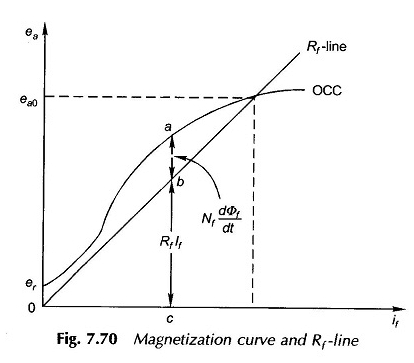
Φf alan akışı, sızıntı nedeniyle doğrudan eksen hava boşluğu akışı φd’den daha yüksektir.
Dikkate alınarak

Burada σ dağılım katsayısı olarak bilinir.
Denk. (7.3),


Denklemdeki denklemlerin (7.110) ve (7.111) yerine geçmesi. (7.109),

NFPAG ile pay ve paydayı çarpın
Veya
Pag, hava / sonrası yürüyüşün geçirgenliğidir 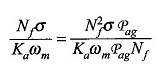
Sayıcının alan endüktansının, LF’nin doymamış değeri olduğu ve payda hava boşluğu hattının eğimi olduğu kolayca kabul edilir. Her ikisi de sabittir. Bu yüzden, 
Bu integral, EA’ya karşı 1 / (ea – rf) yolundaki alanların özetlenmesi ile grafiksel olarak değerlendirilebilir. Bu yaklaşım EA’yı zamana karşı çizmek için kullanılır.
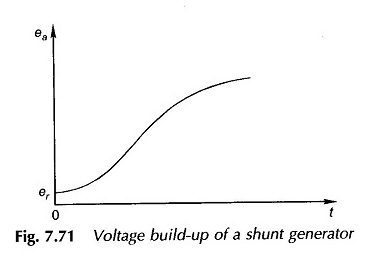
Üretilen EMF’nin vakum değerine ulaşması için gereken teorik zaman, EA0 sonsuz olacaktır; Bu nedenle, pratikte, 0.95 EA0’a ulaşmak için gereken süre EA0’a ulaşmak için gereken süre olarak alınır. EA’nın zaman içinde varyasyonu Şekil 7.71’de çizilmektedir.
Cevap oldukça yavaş çünkü sadece küçük voltaj farklılıkları (= ea – rfif) akış birikimine (φf) katkıda bulunur.