CC Motor Kapalı Döngü Kontrolü:
CC motorunun kapalı döngü kontrolü – Bir sistemin dinamik davranışı bir dizi diferansiyel denklemle tanımlanır. Birçok kez, bu denklemlerin çözümü, zor bir görev olabilecek evrişim integrallerinin değerlendirilmesini gerektirir.
Bu gibi durumlarda, daha basit bir analiz, Laplace dönüşümleri kullanılarak transfer fonksiyonları kullanılarak mümkün hale getirilir.
Tüm başlangıç koşullarının sıfır olduğu varsayılarak, çıkış değişkeninin Laplace dönüşümünün giriş değişkenine dönüşümüne oranı gibi doğrusal değişmez sistemler için bir aktarım fonksiyonu tanımlanır.
Bir veya daha fazla parametreye sahip doğrusal olmayan sistemler, değişen süreye aktarma işlevlerine sahip olamaz, çünkü Laplace dönüşümü onlar için mevcut değildir. Bununla birlikte, Lies olmayan eğitim sistemleri doğrusallaştırılabilir ve doğrusal geri bildirim teorisi uygulanabilir.
Bu sistemler blok diyagramlar veya sinyal akış grafikleri ile temsil edilebilir. Blok diyagramının yaklaşımında, bir blok girişi ve çıkışı ile bir bileşenin işlevini temsil eder. Bileşen aktarım fonksiyonu blokta yazılmıştır. Böylece, transfer fonksiyonu formda
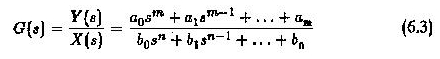
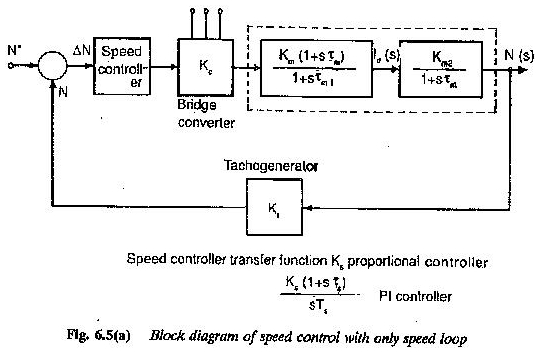
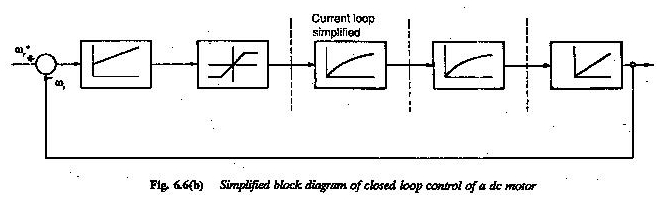
Aktarım fonksiyonunu tanımlarken, tüm diferansiyel denklemleri basit cebirsel denklemlere dönüştürdüğü için Laplace dönüşümü kullanılmıştır. Şekil 6.5, bir tahrik sistemindeki bir DC motorunun bir blok diyagramını temsil eder.
Motor, bir giriş değişkeni olarak bir takviye voltajına ve çıkış değişkeni olarak hıza sahiptir. Aktarım fonksiyonu blokta yazılmıştır.
Aktarım fonksiyonu, sistemin davranışını tanımlayan tüm diferansiyel denklemlerden türetilir. Bununla birlikte, sistemin iç fiziksel yapısını ilgilendirmez.
Farklı fiziksel sistemler benzer transfer fonksiyonlarına ve benzer dinamik davranışlara sahip olabilir. Aktarım işlevi sistem parametreleri açısındandır ve bir sistem özelliğidir. Girişin büyüklüğüne veya doğasına bağlı değildir. Payda’daki en yüksek S gücü sistemin sırasını temsil eder.
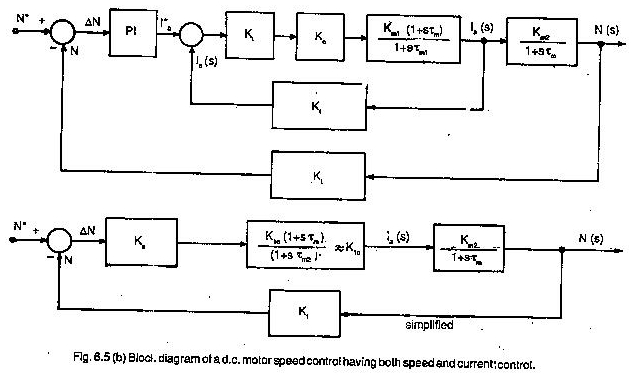
Aktarım işlevleri tarafından sunulan basitliği göstermek için aşağıdaki gibi basit bir örnek verilmiştir.
Örnek:
Şekil 6.6’da gösterildiği gibi iki RC devresi kaskada bağlanır.
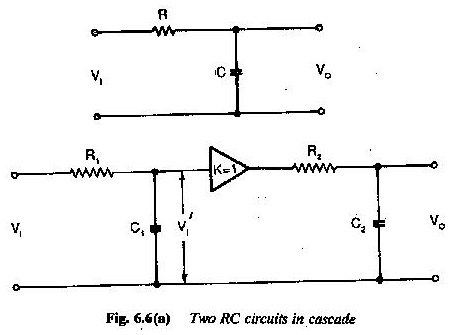
Giriş bir adımdır
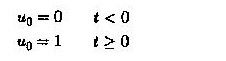 Amplifikatör, aralarında bir CC bağlantısı olarak çalışmak için kullanılır. U2’nin zamansal varyasyonunu belirleyin. Biliyoruz
Amplifikatör, aralarında bir CC bağlantısı olarak çalışmak için kullanılır. U2’nin zamansal varyasyonunu belirleyin. Biliyoruz
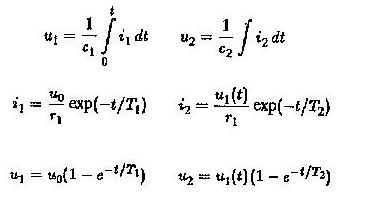
U2 / UO oranı, evrişimin integrali değerlendirilerek elde edilir
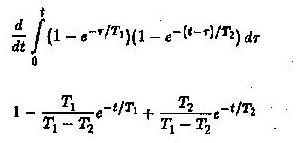
Basamaklı bir RC devresi daha verilen devreye eklenirse – U2 / U0’ın değerlendirilmesi çok zordur.
Öte yandan, transfer fonksiyonunun yaklaşımı kullanılırsa,
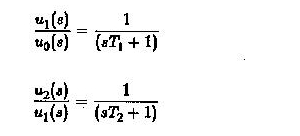
Bu denklemleri kullanarak,

çok kolay değerlendirilebilir

kısmi bir fraksiyon genişlemesi kullanımı olarak.