Geçiş CC motor analizi:
Başlangıç, frenleme, hız değişimi ve yük değişikliği, bir endüstriyel oyuncuda yaygın olarak meydana gelen sürekli akım motorunun geçici analizidir.
Kişi, bu geçiş işlemlerinde sürüş motorunun mevcut, torku ve hızının zaman içinde nasıl değiştiğini bilmekle ilgileniyor.
Bunlardan biri, özellikle motor ısıtmasından sorumlu olanları ve DC motorunun geçici analizinin tamamlanması için geçen süre, enerji kayıplarını bilmekle de ilgilenmektedir.
Bu bilgiler, tasarımcı tarafından motorun uygun bir gösterimini, kontrol ekipmanının doğasını ve türünü ve çalışma takvimini ve koruma cihazlarının ve parametrelerinin türlerini seçmesi için gereklidir.
CC motorların dinamik eşdeğer devreleri Şekil 5.12’de temsil edilmektedir. Kaynak Voltajı V IA ve geri çekilme EMF motoru takviyesinin akımı, bunların değişken miktarlarda anlık değerler olduğunu vurgulamak için kasanın altındaki harflerle belirlenir.
B ve J, sırasıyla NM / RAD / Sec’de viskoz sürtünme katsayısı ve motor şaftında belirtilen motorun motor sisteminin KG-M2’sinde polar atalet momentidir.

Geçiş takviye devresinin voltaj denklemi tarafından verilir

Motor yük sisteminin dinamikleri

Daha öte
![]()
DC motorunun yukarıdaki geçiş analizi herhangi bir DC motoru için geçerlidir. Alan akımı sabit tutulduğunda, heyecanlı bir motor olması durumunda, akış sabit kalır ve (5.16) ve (5.17) doğrusal diferansiyel denklemlerdir.
Bir seri motor durumunda, manyetik devrenin doygunluğu nedeniyle, akış takviye akımının doğrusal olmayan bir fonksiyonudur ve sonuç olarak (5.16) ve (5.17) doğrusal olmayan diferansiyel denklemlerdir.
Manyetik devre doygunluğu ihmal ederek sözde doğrusal olsa bile, (5.16) ve (5.17), E’nin IA ve ωM ürünü ile orantılı olması ve T ile orantılı olması nedeniyle doğrusal olmayan diferansiyel denklemlerdir.
Bu nedenle, seri bir seri için, bu denklemler 4. sıralı Rungekutta yöntemi veya öngörücü düzeltici yöntemi kullanılarak dijital olarak çözülemez.
Uyarılmış motorun olağandışı kontrol ile ayrı ayrı geçiş analizi:
Alan akımı sabit tutulduğunda, akış sabit kalır. Denklemlerde sabit bir k ile keφ değişimi. (5.16) ila (5.18),

Denklemin farklılaşması. (5.20) verir
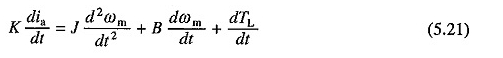
Denklemde ikame. (5.19) (5.21) dia / dt ve yeniden düzenleme için terimler
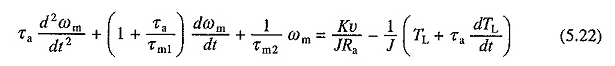
Denklemin farklılaşması. (5.19) verir

Denklemde ikame. (5.20) Denklemin DΩM / DT için. (5.23) ve terimleri yeniden düzenleyin
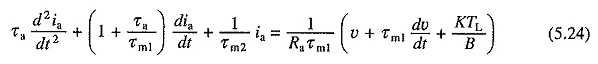
Veya


(5.22) ve (5.24) denklemleri ikinci -orantılı doğrusal diferansiyel denklemlerdir ve uygun başlangıç koşulları biliniyorsa çözülebilir. IA vs t ilişkisi denklemden alındıktan sonra. (5.24), t vs t ilişkisi hesaplanabilir.
Uyarmanın kontrolü ile uyarılmış motorun başlangıcının geçiş analizi:
Başlangıç sürecinin geçiş analizi, yukarıda belirtilen denklemlerin nasıl kullanıldığını göstermek için dikkate alınacaktır.
Motorun, sabit bir şarj torku TL’ye karşı terminallerinden etkilenen sabit bir voltaj v ile ve takviye devresinde sabit bir dirençli RA ile başlatıldığı varsayılacaktır.
Motorun sadece gelişmiş torku şarj torkunu aştıktan sonra başladığını varsaymak olağandır. Çünkü bu motor akımı tarafından verilen değere ulaşmalıdır

Motor güç kaynağına bağlandığında, akımın başlangıç değeri sıfırdır ve olağandışı devrenin endüktansı nedeniyle, değerine ulaşmak belirli bir zaman alır.
Geçiş yanıtının ilk aralığı olarak nitelendirilecek olan tüm bu dönem boyunca, motor durur ve bu nedenle arka EMF sıfır kalır. Motor basit bir RA – yük gibi davranır. Bu nedenle akımı tarafından verilir

İkinci geçici tepki aralığı, akım değerine ulaştıktan sonra başlar. V ve TL sabit olduğundan, DV / DT ve DTL / DT sıfır olacaktır. Bu değerlerin denklemlerde yerine geçmesi. (5.22) ve (5.24)
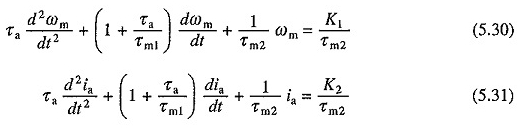
Veya
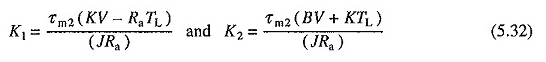
K1 ve K2, TL’ye eşit bir yük torku ile hız ve akım akımının kalıcı değerlerini temsil eder.
Denklemlerin çözümü için gerekli başlangıç koşulları. (5.30) ve (5.31)
![]()
Bu aralığın başında, motor torkunun denklemden yük torkuna eşit olduğu göz önüne alındığında. (5.17)

Denklemden daha fazlası. (5.16)

Eşit çözümler. (5.30) ve (5.31) (5.33) ila (5.35) tarafından verilen başlangıç koşulları ile forma sahip olacaktır:

α1 ve a2’nin karakteristik denklem kökleri olduğu ve
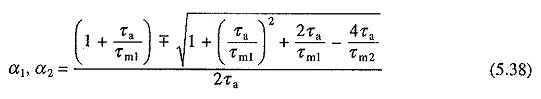
Yukarıdaki denklemlerin, ikinci aralığın başlangıcında zamanın ölçülmesiyle türetildiğine dikkat edin.
1000 kW’dan az olan motorlar için, α1 ve a2 kökleri genellikle gerçektir.
Bir helikopter ve bir DC motoru tarafından sağlanan bir geçiş analizinde olduğu gibi, takviye devresine bağlı harici bir endüktansla daha büyük ve orta boyutlu motorlar için, kökler karmaşık olabilir.
Kökler gerçek olduğunda, başlangıç için ωm vs t ve ia vs t eğrilerinin doğası Şekil 5.13 (a) ‘da temsil edilmektedir.
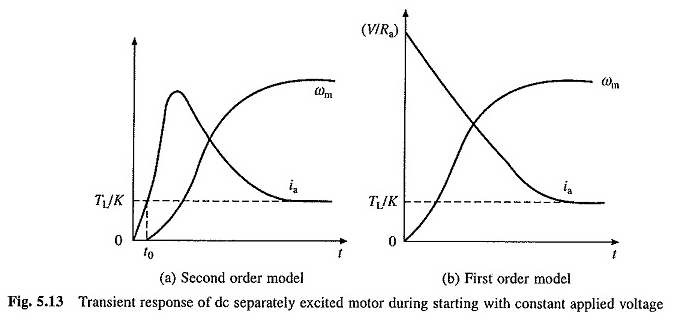
Küçük motorlarda τA, takviyenin sarılmasına büyük bir direnç nedeniyle çok küçüktür. Bu nedenle göz ardı edilebilir. Denklemlerde τa = 0’ın yerine geçme. (5.30) ve (5.31)
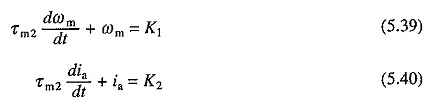
Τa = 0’dan akım sıfır sürede V / RA değerine gider. Böylece, başlangıç koşulları
![]()
Eşit çözümler. (5.39) ve (5.40) verim

Bu denklemlere kıyasla T ve AI eğrilerine göre ωM’nin doğası Şekil 5.13 (6) ‘da temsil edilmektedir.
Heyecanlı motorun dinamik frenlemesinin geçiş analizi ayrı ayrı:
Motor şaftına sabit bir TL aktif yükünün hareket ettiği varsayılmaktadır. Geçiş hızı ve akım denklemleri, olağandışı devrenin direnci için yeni bir değer ve denklemlerde v = 0’ın yerine geçerek elde edilebilir. (5.30) ve (5.31). Verir

Burada da – K3 ve K4 denge durumundaki hız ve akım değerlerini temsil eder. Bu kalıcı işlem, aktif TL yükleme torkunun motoru ters yönde sürmeye yetkili olduğunda gerçekleşecektir. Bu denklemlerin çözümü için gerekli başlangıç koşulları aşağıdaki gibi elde edilir:
Frenlenmenin başlamasında, motorun bir TL yük torkuyla denge durumunda çalıştığı varsayılmaktadır. Sonra denklemden. (5.30)
![]()
Genel bir durum için, K1 başlangıç hızı olarak düşünülmelidir.
Frenleme, takviye devresiyle veya açılmadan uygulanabilir. Açık olmadığında, otomobil frenlemeye geçtiğinde, takviye akımının sürekliliği, daha sonra akımın başlangıç değeri denklemden korunacaktır. (5.31), K2 olacaktır.
Ancak, açıksa, akımın başlangıç değeri sıfır olacaktır. Burada, geçiş sırasında açık olduğunu varsayıyoruz. BU YÜZDEN
![]()
Şimdi Denklemlerden. (5.19) ve (5.20), V = 0, IA = 0 ve ωm = K1 yerine geçerek.
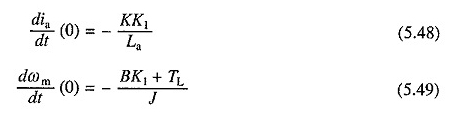
Eşit çözümler. (5.43) ve (5.44) (5.46) ila (5.49) ‘nın başlangıç koşullarına sahip:
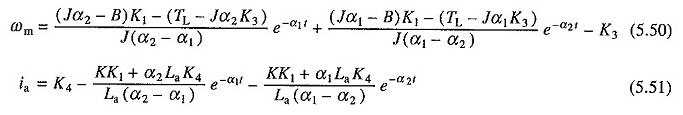
burada α1 ve a2 denklem ile verilir. (5.38).
Gerçek a1 ve a2 durumunda dinamik fren altında geçici yanıtın doğası, Şekil 5.14’te gösterilmektedir.
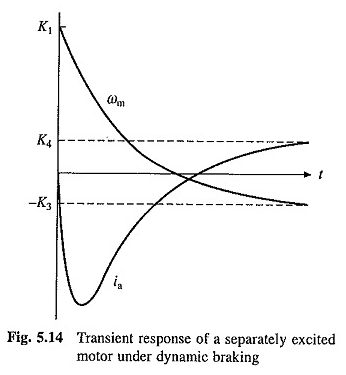
Fiş -in işleminin geçiş denklemleri (5.19), (5.20), (5.22) ve (5.24) ikame – V için elde edilir.
Geçiş operasyonları sırasında enerji kayıpları:
Motordaki ve motor takviye devresindeki dirençlerdeki enerji kayıpları, geçici çalışma periyodunda, motorun ve direncin uygun notlarını seçmek için gereklidir. Geçiş sürecinin verimliliğini ve verimliliğini hesaplamak için de gereklidirler.
Denklemin her iki tarafını da çarpın. (5.16) IA tarafından

Viskoz sürtünme torku TL yük torkunun bir parçası olduğundan, denklemimiz var. (5.17)

İkame denklemleri. (5.18) ve (5.53) ‘de (5.52) ve sonuçta ortaya çıkan denklemin iki tarafının zaman verimine karşı entegre edilmesi
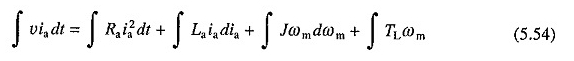
Bu denklem, bir geçiş işlemi sırasında kaynak tarafından sağlanan toplam enerji üzerinde, takviye devresinin direncinde bir parça boşa harcandığını, ikinci kısmının takviye devresinin endüktansında saklandığını, üçüncü kısmının mekanik parçaların ataleti içinde saklandığını ve geri kalanın yük tarafından tüketildiğini öngörüyor.
Takviye devresinin endüktansında depolanan enerji genellikle diğer enerji terimlerine kıyasla düşüktür ve bu nedenle daha sonraki analizde ihmal edilecektir.
Motorun sabit bir V voltajı V ve TL şarj torkuyla başlaması şimdi dikkate alınmaktadır.
İtibaren

burada ωm0 yüksüz ideal hızdır. Denklemler. (5.54) ve (5.55)

Denklem (5.56), makinenin takviye devresinin direncinde enerji kaybı için bir ifade verir. Yük olmadan başladığında, nihai hız (denge durumu) ωm0 olacaktır. Bu nedenle, herhangi bir E0 yük koşulunda enerji kaybı

Yüksiz başlangıç sırasında motor takviye devresindeki enerji kaybının, motorun döner kısımlarında sabit bir durum hızında depolanan kinetik enerjiye eşit olduğunu belirtmek ilginçtir.
Buna ek olarak, başlangıç işleminin süresi, civciv hızının doğası ve motor hızı akımının özelliklerinden, başlangıç direncinin aşamalarının sayısı ve her adımda yeniden listenin değerinden bağımsızdır.
Ωm0, denklemin RHS üzerindeki ilk terim olan motor şaftındaki TL yükü ile denge durumundaki hızdan çok farklı olmayacaktır. (5.56) yaklaşık olarak herhangi bir yük altında başlangıç sırasında bakır kaybını temsil eder ve E0 hakkında söylenenler de bu terim için geçerlidir.
İkinci terim, motor hız yükünün özelliklerine ve başlangıç direncinin değerine bağlıdır. Bu terim, Şekil 5.15’in gölgeli alanı ile temsil edilmektedir.

Yukarıda belirtildiği gibi, (5.56) sağ tarafındaki ilk terim, başlangıç direncindeki değişiklik ile değişmeden kalır. Bununla birlikte, daha düşük bir başlangıç gerilim yöntemi ile düşürülebilir. Kaynak gerginliğinin bir dizi eşit adımda uygulandığı durumu düşünün. MTH bakır kaybının ilk kısmı
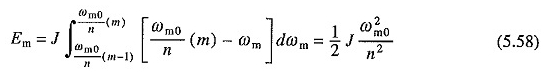
Bakır kaybının bu kısmı tüm n adımlarda aynı olacağından, başlangıçta toplam bakır kaybı olmaz.

Bunun denklemle karşılaştırılması. (5.57), yüksüz bakır kaybının bir n faktörü azaldığını göstermektedir.
Daha sonra reostatik frenleme sırasında kaybı inceleyelim. V = 0’ın yerine geçerek, ihmal ederek ve yük torkunun sabit ve TL’ye eşit olduğu varsayılarak, aşağıdaki denklem (5.52) ve (5.53) ‘den türetilebilir.
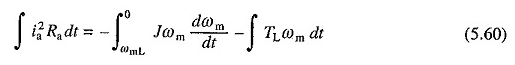
Fren yapmadan önce, motorun bir ωML hızında pasif bir şarj torku TL’ye karşı denge durumunda çalıştığı varsayılmıştır. EQ entegrasyonunda. (5.60) işlenmiş

Bu denklem, yükün depolanan kinetik enerjinin bir kısmını emdiğini ve geri kalanının bakır kaybı şeklinde dağıtıldığını gösterir.
Tıkanma için, denklemlerde – v ve = 0 için —V ikamesi üzerine. (5.52) ve (5.53) Bakır kaybı için aşağıdaki denklem elde edilir
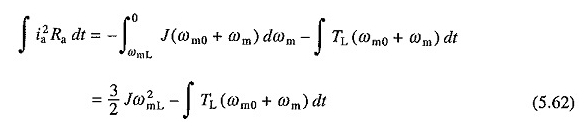
Denklemler. (5.61) ve (5.62) Fren ve dinamik fiş altında yüksüz bakır kayıpları sırasıyla 1/2 JΩ20 ve 3/2 JΩ20 olacaktır. Böylece, bağlantı sırasındaki kayıp, dinamik frenleme sırasında bunun üç katı olacaktır.
Döner parçaların kinetik enerjisinden elde edilen fiş -in enerjisinin sadece 1/2 jΩ2m0 olduğu göz önüne alındığında, geri kalanı jω2m0 güç kaynağından alınır.
Heyecanlı motorun saha kontrolü ile ayrı ayrı geçiş analizi:
Ya sürekli takviye gerginliği. ŞİMDİ
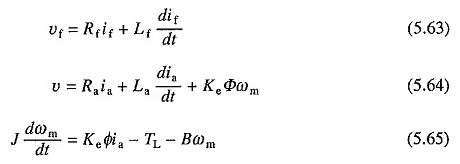
Burada φ, IF’nin doğrusal olmayan bir işlevidir. Doygunluk ihmal edilirse ve φ bununla orantılı olması gerekiyorsa, (5.64) ve (5.65)

burada k ′ = kekφ.
İki değişkenin (5.66) ve (5.67) ürününü içeren k′ifωm ve k′ifia terimleri nedeniyle, doygunluk ihmal edilmiş olsa bile doğrusal olmayan denklemlerdir.
Böylece, bu analiz 4. runege-kutta ve prediktif-köşeler yöntemleri gibi doğrusal olmayan diferansiyel denklemleri çözmek için dijital yöntemler kullanılarak gerçekleştirilebilir.
Takviye akımı sabit tutulduğunda arazi kontrolüne sahip özel bir durum meydana gelir. Daha sonra, motor yük sisteminin dinamikleri denklem tarafından tanımlanır. (5.63) aşağıdaki denklemle:

burada ka = kekφia ve ia takviye akımıdır.
Denklemin. (5.68) IF ve DIF / DT’nin ifadesi elde edilebilir. Bunları denklemde değiştirin. (5.63) ve “terimler verir

Veya

Motor, denklem kullanılarak geçiş yanıtı için analiz edilebilir. (5.69) başlangıç koşullarının bilinmesi şartıyla. Ωm’nin başlangıç değeri, geçiş noktalarından hemen önce denge durumuna ve dΩm / dt’nin başlangıç değeri denklemden hesaplanmadan önce denge durumuna bilinecektir. (5.68).

