Elektrik tahrik sistemindeki CC motor sinyal akış grafiği:
Yukarıda tartışılan elektrikli sürüş sisteminin blok diyagramının temsilindeki CC motor sinyal akış grafiği, sadece bir giriş ve çıkışı olan bileşenlere sahip basit sistemler için yeterlidir.
Bir sistem karmaşık olduğunda, birçok değişkene sahip, blok diyagramını azaltmak gerçekleştirmek çok zor bir görev haline gelebilir.
Bu gibi durumlarda, sistemin genel giriş-çıktı ilişkisinin bir azaltma yapmaya gerek kalmadan belirlenebileceği bir yönteme sahip olmak avantajlı olabilir.
Böyle bir yöntem, sinyal akışına yönelik çizgi segmentlerine sahip sinyal akış grafiği ile bir sistemi temsil ederek sunulur. Değişkenler arasındaki giriş-tedarik ilişkisini belirlemek için bir kazanç formülü mevcuttur.
Daha önce belirtildiği gibi, bir sistem bir dizi diferansiyel denklemle temsil edilebilir.
Bu denklemlerin, dal adı verilen yönlendirilmiş çizgi segmentleri vasıtasıyla birbirine bağlanan düğümler aracılığıyla resimsel gösterime, sistemin sinyal akışının grafikleri denir.
Bir grafiğin düğümü bir sistem değişkenini temsil eder ve bir dal üzerinde belirtilen çarpma faktörü ile tek bir çarpan görevi görür.
Dallar, elektrik tahrik sistemindeki sürekli akım motorunun ok başı yönünde sinyal akışının bir grafiğine izin veren tek yönlü elemanlardır ve bir blok diyagramındaki bloklara eşdeğerdir.
Çok değişkenli bir sistem, durum denklemleri ile temsil edilir
![]()
Böyle bir sistemi temsil etmek için elektrik tahrik sistemindeki bir CC motor sinyal sinyal akış grafiği kullanılabilir. Bir CC motorunun durum denklemleri ayrı ayrı uyarılır ve sinyal akış grafiği sunulur.
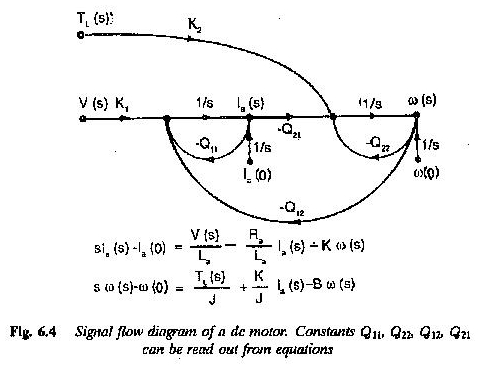
Elektrik tahrik sistemindeki bir CC motor sinyal akış grafiği, bir blok diyagramı tarafından sağlanan aynı bilgileri verir, ancak birkaç avantajı vardır. Çok değişkenli sistemler çok kolay temsil edilebilir. Basit akış grafikleri, inceleme ile film ilişkileri yazmanıza olanak tanır.
Sinyal akışını kullanarak çok değişkenli sistem denklemleri için zamansal alan çözümü basittir. Durum geçiş matrisini ve evrişim integrallerini değerlendirmek gerekli değildir.
Girişin etkisi normal olarak grafiğin giriş ilişkilerinin formülasyonunda desteklenir.
Bir çıkış değişkenini bir giriş değişkenine bağlayan Mason Kazanç Formülü,

Veya
PK, dalların sinyalin akışı yönünde sürekli ardıllığı olarak tanımlanan ve sadece bir kez bir düğümle karşılaşan kazanan kazançtır.
PK yolunun cofaceur ΔK
Δ grafiğin belirlenmesi