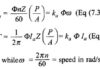Contrôle de boucle fermée du moteur CC:
Contrôle de boucle fermée du moteur CC – Le comportement dynamique d’un système est décrit par un ensemble d’équations différentielles. À de nombreuses reprises, la solution de ces équations nécessite l’évaluation des intégrales de convolution qui peuvent être une tâche difficile.
Dans de tels cas, une analyse plus simple est rendue faisable par l’utilisation de fonctions de transfert utilisant des transformations de Laplace.
Une fonction de transfert est définie pour les systèmes invariants linéaires comme le rapport de la transformée de Laplace de la variable de sortie en transformée de Laplace de la variable d’entrée, en supposant que toutes les conditions initiales sont nulles.
Les systèmes non linéaires avec un ou plusieurs paramètres variant le temps ne peuvent pas avoir de fonctions de transfert car la transformée de Laplace n’existe pas pour celles-ci. Cependant, les systèmes d’entraînement ayant des non-lincarités peuvent être linéarisés et la théorie de la rétroaction linéaire peut être appliquée.
Ces systèmes peuvent être représentés par des diagrammes de blocs ou des graphiques d’écoulement de signal. Dans l’approche du schéma de bloc, un bloc représente la fonction d’un composant avec son entrée et sa sortie. La fonction de transfert du composant est écrite dans le bloc. Ainsi, la fonction de transfert est de la forme
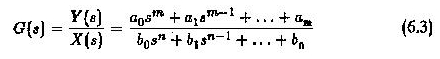
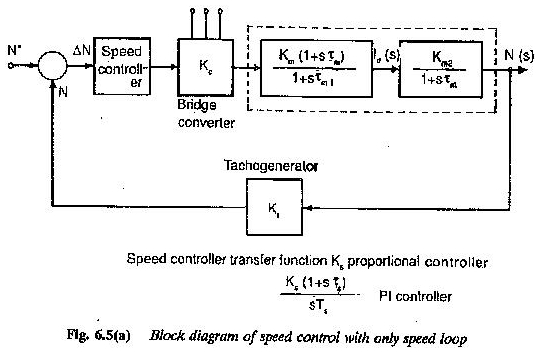
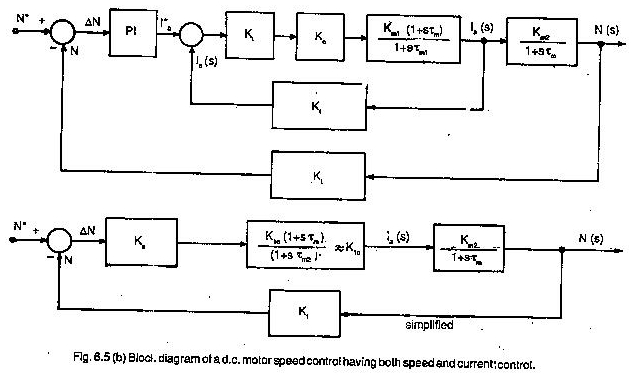
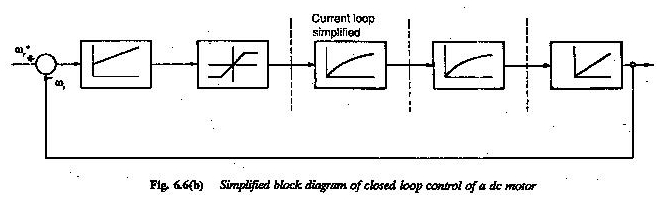
Tout en définissant la fonction de transfert, la transformation de Laplace a été utilisée car elle transforme toutes les équations différentielles en équations algébriques simples. La figure 6.5 représente un schéma de bloc d’un moteur à courant continu dans un système d’entraînement.
Le moteur a une tension d’armature en tant que variable d’entrée et vitesse comme variable de sortie. La fonction de transfert est écrite dans le bloc.
La fonction de transfert est dérivée de l’ensemble des équations différentielles qui décrivent le comportement du système. Il ne concerne cependant pas la structure physique interne du système.
Les systèmes physiques différents peuvent avoir des fonctions de transfert similaires et également un comportement dynamique similaire. La fonction de transfert est en termes de paramètres du système et est une propriété du système. Cela ne dépend pas de l’ampleur ou de la nature de l’entrée. La puissance la plus élevée de S dans le dénominateur représente l’ordre du système.
Un exemple simple est donné dans ce qui suit pour montrer la simplicité offerte par les fonctions de transfert.
Exemple:
Deux circuits RC sont connectés en cascade, comme le montre la figure 6.6.
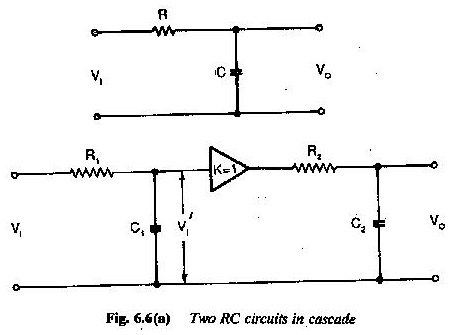
L’entrée est une tension de pas
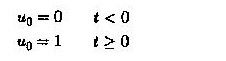L’amplificateur est utilisé pour fonctionner comme un couplage CC entre eux. Déterminez la variation temporelle de U2. Nous savons
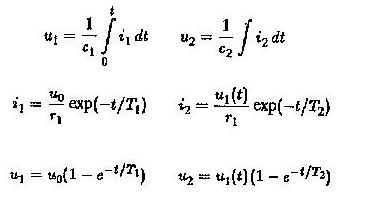
Le rapport U2 / UO est obtenu en évaluant l’intégrale de la convolution
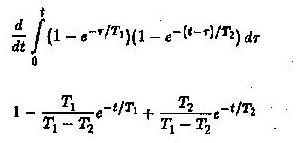
Si un circuit RC de plus est ajouté en cascade au circuit donné – l’évaluation de U2 / U0 est très difficile.
D’un autre côté, si l’approche de la fonction de transfert est utilisée, nous avons
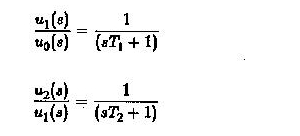
En utilisant ces équations, nous avons
peut être très facilement évalué
comme utilisant une expansion de fraction partielle.