Fonction de transfert du moteur à courant continu contrôlé par l’armature:
La vitesse d’un moteur à courant continu peut être contrôlée en faisant varier la tension appliquée à l’armature d’un moteur à courant continu. Un moteur à courant continu excité séparément avec une tension armature variable trouve l’application en tant que moteur d’entraînement dans un lecteur de vitesse variable.
Fonction de transfert moteur à courant continu – fonction de transfert mcc
La tension d’armature variable est fournie par un redresseur contrôlé en phase. Le schéma d’une fonction de transfert du moteur CC contrôlé par armature est illustré à la figure 6.7.
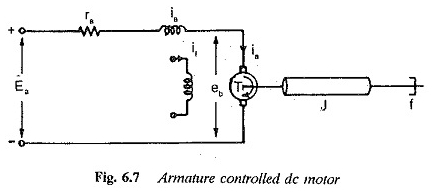
Le couple développé par le moteur CC
![]()
où
Φ est un flux d’espace aérien
IA est un courant d’armature
K est une constante
Négligeant les effets de la saturation et de la réaction d’armature, nous avons le flux d’espace d’air proportionnel au courant de champ. C’est ![]()
Car si est constant, le couple développé est donné par
![]()
où kt est le moteur constant. La tension d’armature EA est fournie par le convertisseur de thyristor. L’équation du circuit d’inhabituel est donnée par 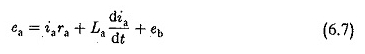
EB en Eq. 6.7 est l’EMF rotationnel (arrière) induit dans l’armature et est proportionnel au produit de la vitesse et du flux. Mais, le flux du moteur est constant. Par conséquent, l’équation dynamique du moteur donnant l’équilibre du couple peut être écrite comme 
En supposant que les conditions initiales sont nulles, les transformations de Laplace des Eqs 6.7, 6.8 et 6.9 peuvent être écrites comme
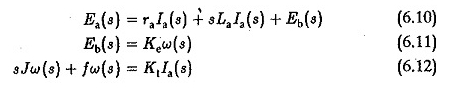
Prenant EA (S) comme entrée et W (S) comme sortie, la fonction de transfert W (S) / EA (S) peut être obtenue en éliminant les LA (s) des équations et est donnée par

Le diagramme de bloc donné sur la figure 6.8 (a) représente l’équation. 6.13. Cela peut finalement être réduit à un seul bloc donné sur la figure 6.8 (b).
Normalement, l’inductance de l’armature LA est très petite et peut être négligée. La fonction de transfert dans ce cas est donnée par

On peut voir que l’EMF arrière affecte l’amortissement du système. Une fonction de transfert entre la vitesse et le couple de charge peut être dérivée en supposant que l’autre entrée EA est nulle. Dans ce cas, l’équation dynamique serait
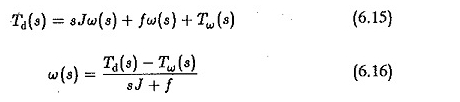
Mais à partir des Eqs 6.10 et 6.11, nous avons

Substituant dans l’équation. 6.15 et simplifier que nous obtenons
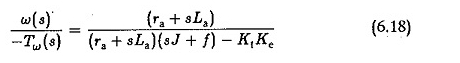

où k est constant. Si les pôles de cette fonction de transfert sont des conjugués complexes, le changement de vitesse pour un changement dans le couple de charge est oscillatoire.
