Funzione di trasferimento del motore CC controllata dal rinforzo:
La velocità di un motore a CC può essere controllata variando la tensione applicata al telaio di un motore CC. Un motore a CC eccitato separatamente con una tensione di rinforzo variabile trova l’applicazione come motore di azionamento in un lettore a velocità variabile.
La tensione di rinforzo variabile è fornita da un raddrizzatore controllato in fase. Il diagramma di una funzione di trasferimento del motore CC controllato dal rinforzo è illustrato nella Figura 6.7.
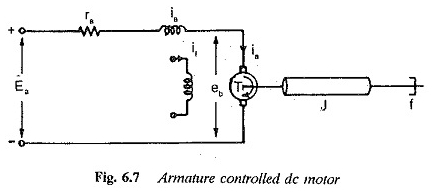
La coppia sviluppata dal motore CC
![]()
O
Φ è un flusso di spazio aereo
Ia è una corrente di rinforzo
K è una costante
Trascurando gli effetti della saturazione e della reazione della reazione, abbiamo il flusso di spazio aereo proporzionale alla corrente di campo. È ![]()
Perché se la coppia sviluppata è data da
![]()
Dove KT è il motore costante. La tensione di rinforzo EA è fornita dal convertitore tiristore. L’equazione del circuito insolito è data da 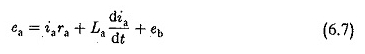
EB in Eq. 6.7 è il rotazionale EMF (posteriore) indotto nel telaio ed è proporzionale al prodotto e al prodotto di flusso. Tuttavia, il flusso del motore è costante. Di conseguenza, l’equazione dinamica del motore che fornisce l’equilibrio della coppia può essere scritta come 
Supponendo che le condizioni iniziali siano zero, le trasformazioni del Laplace di Eqs 6.7, 6.8 e 6.9 possono essere scritte come
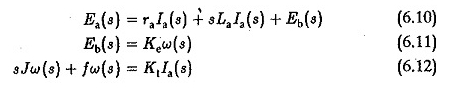
Prendendo EA (s) come input e W (s) come output, la funzione di trasferimento W (s) / EA (s) può essere ottenuta eliminando le equazioni ed è data da

Il diagramma a blocchi indicato nella Figura 6.8 (a) rappresenta l’equazione. 6.13. Questo può in definitiva essere ridotto a un singolo blocco indicato nella Figura 6.8 (b).
Normalmente, l’induttanza del rinforzo è molto piccola e può essere trascurata. La funzione di trasferimento in questo caso è data da

Possiamo vedere che l’EMF posteriore influisce sullo smorzamento del sistema. Una funzione di trasferimento tra velocità e coppia di carico può essere derivata supponendo che l’altro ingresso EA sia zero. In questo caso, l’equazione dinamica sarebbe
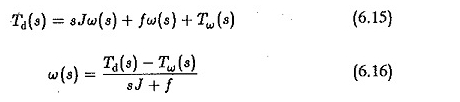
Ma dalle Eq 6.10 e 6.11, abbiamo

Sostituendo nell’equazione. 6.15 e semplificare che otteniamo
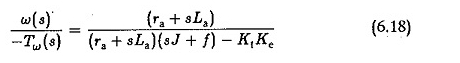

dove k è costante. Se i poli di questa funzione di trasferimento sono coniugati complessi, la variazione di velocità per una variazione della coppia di carico è oscillatoria.



