Moteur CC sans balais:
Le terme moteur CC sans balais est appliqué à de nombreuses configurations de moteurs synchrones AC dans lesquels le contrôle des semi-conducteurs est utilisé pour contrôler les courants du stator tels que le couple maximal est obtenu à une vitesse donnée.
Dans un moteur conventionnel, le contacteur mécanique, le commutateur, maintient le déplacement d’espace de degrés à 90 ° de degrés entre les champs magnétiques du rotor et du stator pour fournir le couple requis.
Théoriquement, les fonctions stator et rotor d’une machine peuvent être inversées, ce qui met le système de terrain sur le rotor.
Il n’y a aucun avantage à gagner si une commutation conventionnelle est utilisée, car les coupes de commutateurs sont fixes et que l’engrenage de la brosse doit tourner à la vitesse du champ du rotor.
La commutation à semi-conducteurs par des transistors ou des thyristors, déclenchée par des capteurs de position, peut cependant remplacer l’engrenage des brosses par une commutation entièrement électronique, dominant de petites machines par une usine de contrôle précieuse.
Dans cette méthode, chaque phase de l’enroulement du stator est énergique séquentiellement par un transistor de puissance (ou thyristor) au moyen d’un signal du capteur de position placé sur le rotor.
En raison du déclenchement de rétroaction en position du rotor des thyristors / transistors, le champ du stator et du rotor reste toujours en synchronisme car la fréquence de déclenchement s’ajuste automatiquement à la vitesse du moteur. La longueur des temps des transistors détermine l’amplitude du couple du moteur.
Ainsi, au moyen de circuits électroniques, les moteurs sans balais peuvent être contrôlés pour un fonctionnement à couple constant et variable.
Les moteurs CC sans balais tout en étant généralement plus chers pour la même note KW, que les manquiers et les moteurs à brosses possèdent certains avantages par rapport aux moteurs conventionnels.
Avantages du moteur CC sans balais:
- Ils nécessitent peu ou pas d’entretien.
- Ils ont une vie opérationnelle beaucoup plus longue.
- Il n’y a aucun risque d’explosion ou de possibilité de rayonnement RF en raison de l’arc.
- Ils ne produisent pas de pinceau ni de particules ou de gaz de commutateur comme sous-produits de fonctionnement.
- Ils sont capables d’opérer soumis dans les fluides, les gaz combustibles et peuvent même être hermétiquement scellés.
- Ils sont généralement plus efficaces que les serviteurs DC de type pinceau ou les moteurs DC conventionnels.
- Ils fournissent une réponse plus rapide et un couple de sortie assez linéaire par rapport à la caractéristique de courant d’entrée, qui se prête aux applications de servo.
Principe de schéma et d’exploitation du moteur CC sans balais:
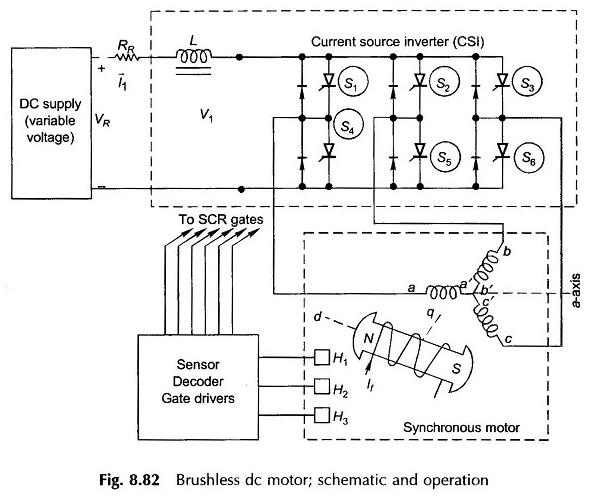
Le diagramme schématique d’un moteur CC sans balais est illustré à la figure 8.82. Il montre également les trois phases du stator (armature) et du rotor avec des axes D et Q indiqués.
Le stator est connecté à une source de courant de tension variable via une inductance et un onduleur comprenant six SCR (S1 à S6). À la place des SCR, le transistor de puissance ou les FET pourraient être utilisés en fonction de la puissance du moteur.
Les diodes sont connectées à travers les SCR pour les protéger de la tension L (di / dt) induite dans la bobine d’armature subissant une commutation.
Les capteurs de position placés sur le rotor fournissent un signal aux décodeurs de capteurs et aux pilotes de grille qui provoquent une séquence de SCR en séquence afin d’être en synchronisme avec la position mécanique du rotor.
Les champs stator et rotor se verrouillent ainsi et restent en synchronisme à n’importe quelle vitesse du rotor.
Les courants de phase idéaux sont des impulsions de ± i duré à 120 °, sélectionnez chaque moitié et déplacés les uns des autres à 120 ° Elect Phase à phase comme indiqué sur la figure 8.83. Les formes d’onde de courant réelles diffèrent des ondes de courant rectangulaires idéales par augmentation et chute progressive.
Un tel onduleur où le courant CA s’écoule sous forme d’impulsions de courant constant est connu sous le nom de servo-invertisseur de courant (CSI).

La séquence de tir de l’onduleur comme le montre la figure 8.83 découle immédiatement des formes d’onde de courant de phase. Pour cette séquence de tir SCR à 120 ° ou 60 °, des codes de capteur espacés sélectionnés sont générés au moyen de capteurs de légers sensibles ou d’effet de hall.
La figure 8.84 illustre le cas de l’espacement de 120 ° dans lequel ces capteurs sensibles à la lumière sont représentés à 120 ° fixes, obtenant la lumière à partir d’une source de lumière fixe.
Le rotor transporte un disque de commutateur avec une découpe de 180 ° de sorte que lorsqu’il tourne avec le rotor, les capteurs lumineux reçoivent une lumière à 180 ° et sont sombres pendant 180 °. Les capteurs produisent la logique «1» tout en recevant une lumière et une logique «0» lors de l’obscurité.
On voit facilement que les trois capteurs (fixes) et le disque de communication (rotatif avec le rotor) produisent une séquence de code du capteur comme indiqué sur la figure 8.83 à partir de laquelle les circuits électroniques génèrent des impulsions de déclenchement pour tirer des SCR dans la séquence comme indiqué sur la figure.
La position relative du disque de communication peut être ajustée WRT les pôles du rotor (axe IEWRT D et Q). Pour la position instantanée du rotor (avec des disques fixés comme indiqué), on constate que le code du capteur va simplement passer de 101 à 100.
La phase «A» est au milieu de son impulsion de courant lorsque le courant se rend de la phase B à c. À cet instant, le champ de stator résultant F̅1 est orienté le long de l’axe A comme le montre la Fig.
8.83 (la direction positive du courant automobile est opposée à la direction positive de la FMF induite); Vérifiez la phase «A» en appliquant la règle de la main droite de Fleming. Le pôle nord du stator est ainsi orienté le long de l’axe a.

Ce pôle Nord pousse le rotor nord pour créer un couple de automobile (l’angle entre le rotor et le stator n-poles est β). Un marqueur d’index peut être fabriqué sur le disque de commutateur qui pointe toujours vers le stator nord alors que le champ du stator tourne en synchronisme avec le rotor.
Cet indice fait un angle γ avec l’axe Q du rotor (axe D en retard de 90 °). Évidemment (β + γ) = 90∘. L’angle peut être ajusté en déplaçant le disque de communication sur l’arbre lié aux pôles du rotor.

Un moteur à courant continu de l’aimant permanent utilisant des capteurs d’effet de salle avec un espacement électoral à 60 ° est illustré à la figure 8.85. Les capteurs génèrent la logique 1 ‘lorsqu’ils sont exposés à N-POLE et «0» sinon. La séquence de code du capteur pour cette arrangement est facilement visualisée et est donnée sur la figure 8.83.
Avec H3 situé le long de l’axe A, le code du capteur à la position du rotor indiqué passe de 000 à 001, ce qui signifie que le courant est au milieu de la conduction pour la phase «A» et il passe de B à c. Ainsi, F1 est dirigé le long de l’axe A ou du stator n-pole est le long de l’axe G IE
γ = 0 (voir Fig. 8.84). Les moteurs à aimant permanent sont généralement ajustés pour cette valeur de γ (cela correspond à β = 90 °, mieux pour la production de couple).
Diagramme de circuit de moteur CC sans balais:
Le modèle de circuit Novotny-Abbas d’un CSI nourri de moteurs CC sans balais est dessiné sur la figure 8.86. Les courants (équilibrés) coulant dans la machine synchrone de la machine DC sans balais configure de la figure 8.82 sont des impulsions rectangulaires AC comme indiqué dans les formes d’onde de la figure 8.83.
Les courants réels sont des impulsions quelque peu arrondies. Notre analyse sera basée sur le courant AC fondamental et les courants harmoniques seront ignorés. Ceux-ci produisent des champs d’air-pap harmoniques spatiaux qui, en tant que champ non stationnaire, le champ du rotor produit un couple zéro net.
Laisser
I1 = courant alimenté à l’onduleur par la source DC
Alors
IM (RMS de phase Current = courant fondamental
= (√6 / π) i1; peut être montré par la série Fourier
Sur la figure 8.86 (a), le modèle de machine synchrone est celui habituel caractérisé par la réactance synchrone à axe direct XD et l’excitation EMF EF où XD et EF varient directement avec la vitesse qui régit la fréquence de fonctionnement.
L’amplitude EF est bien sûr liée au courant du champ du rotor par la caractéristique de magnétisation. Le diagramme de phaseur correspondant est dessiné sur la figure 8.86 (b) où IM, le courant de phase, est dessiné en V (tension de sortie CA / tension de borne de la machine synchrone) par angle φ. Le fonctionnement actuel de premier plan est effectué car il contribue à l’extinction du courant dans la commutation SCR.

Nous allons maintenant créer le modèle AC de CSI avec les conditions:
- Iae = im
- Le paramètre du circuit du modèle est la résistance RAE.
- Ege et Iae sont en phase.
Ces conditions garantiront que cette partie du modèle représente en effet la machine CC équivalente.
On voit également sur la figure 8.84 que l’angle de phase entre i̅m = i̅ae et ef est en effet l’angle γ. Assimilant maintenant la puissance convertie par phase de la machine synchrone à celle de la machine DC équivalente que nous avons

Traduire ce résultat dans le diagramme de phaseur (Fig. 8.86 (b)), il devient clair que V et Ege sont liés par une réactance fictive XE comme indiqué dans le circuit de la figure 8.86 (a). Nous allons maintenant obtenir la relation pour la TEV et Rae. Négliger les pertes d’onduleur
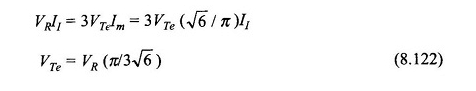
Imaginer un court-circuit à ege c’est-à-dire ege = 0, nous avons
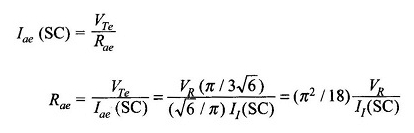
Mais
Vr / i1 (sc) = rr; Résistance interne du redresseur alimentant l’onduleur
Alors
![]()
Caractéristiques du moteur CC sans balais:
En référence à la figure 8.84 (c)
![]()
Comme déjà montré dans l’équation. (8.121)
![]()
Mais EF peut être écrit comme
![]()
où
- Φf = flux / pôle causé par si agir seul.
Substituant les valeurs dans l’équation. (8.124)
![]()
ou

À l’exception de l’effet de Cos γ, cette équation est la même que dans la machine DC conventionnelle.
Le couple développé est donné par
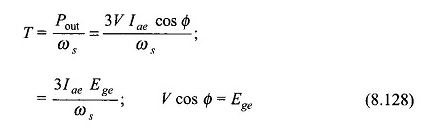
En utilisant l’équation. (8.126), nous obtenons
![]()
Si la caractéristique de l’aimantation est supposée linéaire
![]()
Les équations de vitesse et de couple sont alors

Dans un moteur synchrone, car le courant de champ est réduit, sa PF devient plus à la traîne. Mais dans un moteur CC sans balais (qui est un moteur synchrone avec rétroaction en position de rotor), la diminution du courant de champ si provoque une augmentation de la vitesse selon l’équation.
(8.131) comme dans un moteur CC conventionnel. Cela peut s’expliquer qualitativement par le raisonnement qui suit. En référence à la figure 8.86 comme si elle était diminuée, EF et SO EGE se réduisent et que RAE est très faible, cela provoque une augmentation disproportionnée de IAE = IM.
Le résultat est l’accélération du rotor. L’augmentation de la vitesse du rotor contret la réduction de l’EF et que IM augmente à mesure que la chute de tension IMXD augmente avec l’augmentation de la fréquence de fonctionnement. Le résultat est une opération régulière à une vitesse nouvelle et plus élevée à un PF moins en tête ou même en retard.
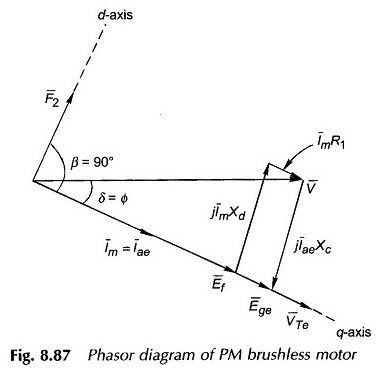
Motor DC sans balais PM:
Le moteur à courant continu de petite taille PM est généralement des types de PM. Dans un tel rotor de moteur, le MMF F2 reste fixe et également l’angle γ dans ces machines est réglé sur zéro, ce qui signifie que F2 et F1 (MMF d’armature) sont déplacés par un angle de 90 ° (mieux pour le couple développé).
De plus, la résistance à l’enroulement de phase R1 n’est pas négligeable et doit donc être ajoutée à RAE dans le modèle DC. Le diagramme de phaseur pour γ = 0 est dessiné sur la figure 8.87 dans laquelle les observations suivantes sont faites
- Xc = réactance capacitive = xd (en amplitude).
- L’angle PF est à la traîne.
La relation des équations. (8.127) et (8.129) pour la vitesse et le couple s’appliquent à l’exception de l’équation. (8.124) modifie désormais en tant que
![]()