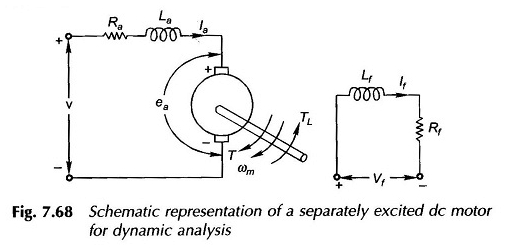
Moteur CC excité séparément pour l’analyse dynamique:
Moteur CC excité séparément pour l’analyse dynamique – les machines CC sont assez polyvalentes et sont capables de donner une variété de caractéristiques VA et à la vitesse-couple par des combinaisons appropriées de divers enroulements de champ.
Analyseurs dynamiques de moteurs électriques
Avec les commandes à semi-conducteurs, leurs vitesses et sorties peuvent être contrôlées facilement sur une large plage pour le fonctionnement dynamique et en régime permanent. En ajoutant le circuit de rétroaction, les caractéristiques de la machine peuvent être encore modifiées. Le but de cette section est d’étudier les machines DC en référence à leurs caractéristiques dynamiques.
Pour l’illustration, considérons la machine CC excitée séparément représentée schématiquement sur la figure 7.68. Pour faciliter l’analyse, les hypothèses suivantes sont faites:
- L’axe de la MMF d’armature est fixé dans l’espace, le long de l’axe Q.
- L’effet démagnétisateur de la réaction d’interrissage est négligé.
- Le circuit magnétique est supposé linéaire (pas d’hystérésis et de saturation). En conséquence, toutes les inductances (qui sont entrées en jeu dans l’analyse dynamique) sont considérées comme constantes.
Les deux paramètres d’inductance apparaissant sur la figure 7.68 sont définis ci-dessous:
- LA = auto-inductance de l’armature causée par le flux d’armature; Ceci est assez petit et peut être négligé sans provoquer une grave erreur dans l’analyse dynamique
- LF = auto-inductance de l’enroulement de champ; il est assez grand pour le champ de shunt et doit être pris en compte
Inductance mutuelle (entre champ et armature) = 0; Parce que les deux sont en quadrature spatiale.
De plus, pour le moteur CC excité séparément pour une analyse dynamique, il est pratique d’utiliser la vitesse en RAD / s plutôt que le RPM.
Appliquer la loi de Kirchhoff au circuit de l’armature,
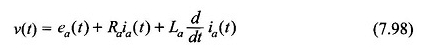
où
![]()
De même pour le circuit de terrain,
![]()
Pour le fonctionnement de l’automobile, le moteur CC excité séparément pour une analyse dynamique pour le système mécanique est

où
J = moment d’inertie du moteur et de charge dans NMS2
D = coefficient d’amortissement visqueux représentant une perte de couple de rotation, nm rad / s
Le stockage d’énergie est associé aux champs magnétiques produits par IF et IA et avec l’énergie cinétique des pièces rotatives. Les équations ci-dessus sont un ensemble d’équations d’état non linéaires (en raison de produits si (t) ωm et si (t) ia (t) avec des variables d’état si, ia et ωm. La solution doit être obtenue numériquement.
Fonctions de transfert et schéma de bloc du moteur CC excité séparément:
Dans le cas linéaire simple de réponse du moteur aux changements de tension d’inmarrure, il est supposé que la tension de champ est constante et que l’état d’équilibre existe sur le circuit de champ, c’est-à-dire si = constant. Les équations (7.98), (7.100) et (7.101) deviennent désormais linéaires comme indiqué ci-dessous

EQS de transformation de Laplace (7.102) et (7.103),
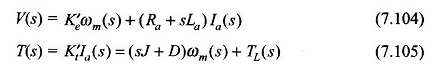
Ces équations peuvent être réorganisées comme 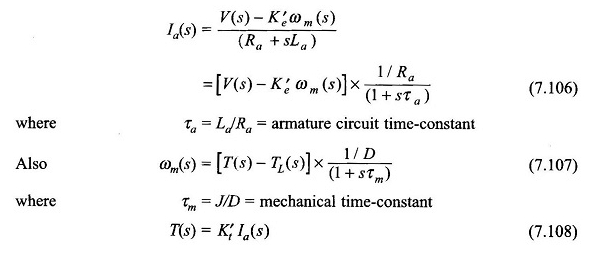
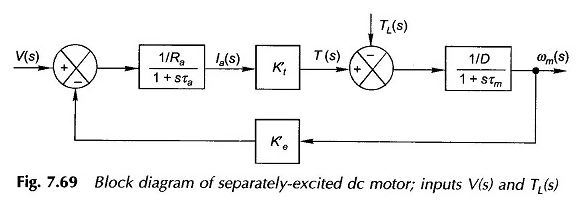
À partir des équations (7.106) – (7.108), le diagramme de bloc du moteur peut être dessiné comme sur la figure 7.69. Il s’agit d’un système de rétroaction de second ordre avec une réponse oscillatoire en général. Il est réduit à un système simple de premier ordre, si LA et donc τa est négligé.
Accumulation de tension du générateur de shunt:
L’explication qualitative du processus d’accumulation de tension dans un générateur de shunt a déjà été discutée. Ici, le traitement mathématique de ce problème sera donné, ce qui se résume en fait à la solution d’une équation différentielle non linéaire.
Se référant à la Fig. 7.70, on voit que pour tout courant de champ, l’interception AB, entre l’OCC et la ligne RF donne la chute de tension causée par le taux de changement de φf et l’interception BC donne la baisse de la résistance au champ. Les deux équilibrent ensemble l’EMF généré EA (négligeant IFRA, la goutte de l’armature). Ainsi 
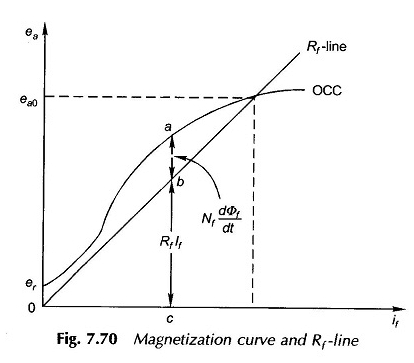
Le flux de champ φf est supérieur au flux d’air-gap à axe direct φd en raison de la fuite.
En tenant compte

Ici, σ est connu comme le coefficient de dispersion.
Rappelant Eq. (7.3),


Substituant les équations (7.110) et (7.111) dans l’équation. (7.109),

Multiplier le numérateur et le dénominateur par NFPAG
où
PAG est la perméance du randonnée à air / poteau 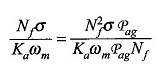
Il est facilement reconnu que le numérateur est la valeur insaturée de l’inductance du champ, LF, et le dénominateur est la pente de la ligne d’air-gap. Les deux sont des constantes. Ainsi, 
Cette intégrale peut être évaluée graphiquement en résumant les zones sur un tracé de 1 / (EA – RF IF) contre EA. Cette approche est utilisée pour comploter EA contre le temps.
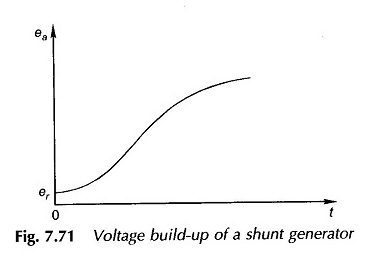
Le temps théorique nécessaire pour que l’EMF généré atteigne la valeur à vide, EA0 serait infinie; Par conséquent, dans la pratique, le temps nécessaire pour atteindre 0,95 EA0 est pris comme le temps nécessaire pour atteindre EA0. La variation de l’EA avec le temps est tracée sur la figure 7.71.
La réponse est plutôt lente car seules les petites différences de tension (= EA – RFIF) contribuent à l’accumulation de flux (φf).