DC -motoroverdrachtsfunctie geregeld door de versterking:
De snelheid van een DC -motor kan worden geregeld door de spanning te variëren die wordt toegepast op het frame van een DC -motor. Een opgewonden DC -motor afzonderlijk met een variabele versterkingsspanning vindt de toepassing als een aandrijfmotor in een speler met variabele snelheid.
De variabele versterkingsspanning wordt geleverd door een gecontroleerde gelijkrichter in fase. Het diagram van een CC -motoroverdrachtsfunctie die wordt bestuurd door versterking wordt geïllustreerd in figuur 6.7.
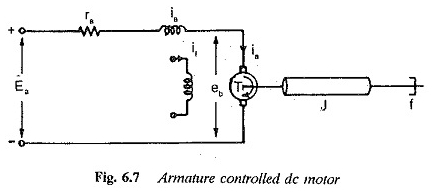
Het koppel ontwikkeld door de CC -motor
![]()
Of
Φ is een stroom van luchtruim
Ia is een stroom van versterking
K is een constante
We verwaarlozen de effecten van verzadiging en reactie van de reactie, we hebben de stroom van luchtruimte die evenredig is aan de veldstroom. Het is ![]()
Omdat als het ontwikkelde paar wordt gegeven door
![]()
waar KT de constante motor is. De EA -versterkingsspanning wordt geleverd door de thyristor -omzetter. De vergelijking van het ongebruikelijke circuit wordt gegeven door 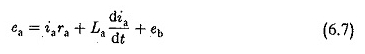
Eb in eq. 6.7 is de EMF -rotatie (achter) geïnduceerd in het frame en is evenredig met het product- en stroomproduct. De motorstroom is echter constant. Bijgevolg kan de dynamische motorvergelijking die het evenwicht van het koppel geeft, worden geschreven als 
Ervan uitgaande dat de beginvoorwaarden nul zijn, kunnen de transformaties van de laplace van vergelijking 6.7, 6.8 en 6.9 worden geschreven als
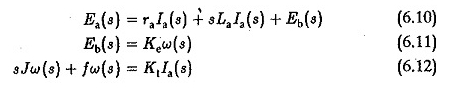
EA (s) als input en w (s) als uitvoer, de overdrachtsfunctie w (s) / ea (s) kan worden verkregen door de vergelijkingen te elimineren en wordt gegeven door

Het blokdiagram gegeven in figuur 6.8 (a) geeft de vergelijking weer. 6.13. Dit kan uiteindelijk worden gereduceerd tot een enkel blok gegeven in figuur 6.8 (b).
Normaal gesproken is de inductie van de versterking erg klein en kan worden verwaarloosd. De overdrachtsfunctie wordt in dit geval gegeven door

We kunnen zien dat de achterste EMF de demping van het systeem beïnvloedt. Een overdrachtsfunctie tussen snelheid en belastingskoppel kan worden afgeleid door aan te nemen dat de andere EA -ingang nul is. In dit geval zou de dynamische vergelijking zijn
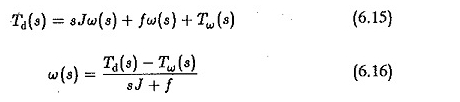
Maar van Eqs 6.10 en 6.11 hebben we

Vervangen in de vergelijking. 6.15 en vereenvoudigen dat we verkrijgen
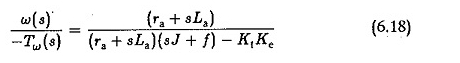

waar k constant is. Als de polen van deze overdrachtsfunctie complexe conjugaten zijn, is de snelheidsverandering voor een verandering in het laadkoppel oscillerend.



