Funkcja transferu silnika DC kontrolowana przez wzmocnienie:
Prędkość silnika prądu stałego można kontrolować, zmieniając napięcie przyłożone do ramy silnika prądu stałego. Podekscytowany silnik DC osobno z zmiennym napięciem wzmacniającym znajduje aplikację jako silnik napędowy w odtwarzaczu o zmiennej prędkości.
Zmienne napięcie zbrojenia jest dostarczane przez kontrolowany prostownik w fazie. Schemat funkcji transferu silnika CC kontrolowanej przez zbrojenie pokazano na rysunku 6.7.
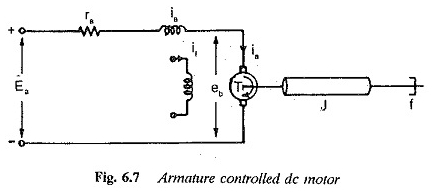
Moment obrotowy opracowany przez silnik CC
![]()
Lub
Φ jest przepływem przestrzeni powietrznej
IA jest prądem zbrojenia
K jest stałym
Zaniedbając wpływ nasycenia i reakcji reakcji, mamy przepływ przestrzeni powietrznej proporcjonalnej do prądu pola. To jest ![]()
Ponieważ jeśli opracowana para jest podana przez
![]()
gdzie KT jest stałym silnikiem. Napięcie wzmacniające EA jest dostarczane przez konwerter tyrystorowy. Równanie nietypowego obwodu jest podane przez 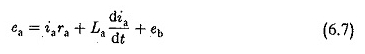
EB w równaniu. 6.7 to obrotowe (tylne) EMF indukowane w ramce i jest proporcjonalne do produktu i produktu przepływowego. Jednak przepływ silnika jest stały. W konsekwencji dynamiczne równanie silnika dające równowagę momentu obrotowego można zapisać jako 
Zakładając, że warunki początkowe wynoszą zero, transformacje laplace Eqs 6.7, 6.8 i 6.9 można zapisać jako
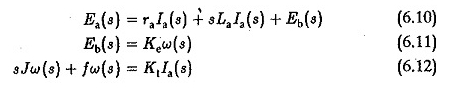
Przyjmując EA (y) jako wejście i W (S) jako wyjściowe, funkcję przeniesienia w (s) / ea (e) można uzyskać, eliminując równania i jest podane przez

Schemat blokowy podany na rysunku 6.8 (a) reprezentuje równanie. 6.13. Można to ostatecznie zmniejszyć do jednego bloku podanego na ryc. 6.8 (b).
Zwykle indukcyjność wzmocnienia jest bardzo mała i może być zaniedbywana. Funkcja transferu w tym przypadku jest podana przez

Widzimy, że tylny EMF wpływa na tłumienie systemu. Funkcję transferu między prędkością a momentem obciążenia można wyprowadzić, zakładając, że drugie wejście EA wynosi zero. W takim przypadku równanie dynamiczne byłoby
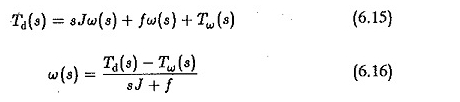
Ale z równania 6.10 i 6.11 mamy

Zastępowanie w równaniu. 6.15 i uproście, że otrzymujemy
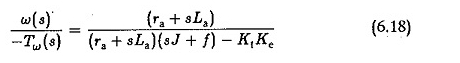

gdzie k jest stałe. Jeśli bieguny tej funkcji transferu są złożonymi koniugatami, zmiana prędkości zmiany momentu obciążenia jest oscylacyjna.



